H&NCTF 2025 部分题目WriteUP
前言
一个人奋战半天拿了个第41,Crypto也没AK,遗憾退场
Crypto
哈基coke
import matplotlib.pyplot as plt |
Arnold变换,可以编写如下代码进行求解: import matplotlib.pyplot as plt
import cv2
import numpy as np
from PIL import Image
def arnold_decode(image, shuffle_times, a, b):
decoded_image = np.copy(image)
h, w = image.shape[0], image.shape[1]
N = h
for _ in range(shuffle_times):
new_image = np.zeros_like(decoded_image)
for x in range(h):
for y in range(w):
ori_x = ((a * b + 1) * x - b * y) % N
ori_y = (-a * x + 1 * y) % N
new_image[ori_x, ori_y, :] = decoded_image[x, y, :]
decoded_image = np.copy(new_image)
return decoded_image
encrypted_img = cv2.imread('en_flag.png')
decrypted_img = arnold_decode(encrypted_img, shuffle_times=6, a=9, b=1)
cv2.imwrite('decrypted_flag.png', decrypted_img, [int(cv2.IMWRITE_PNG_COMPRESSION), 0])

那么可以得到flag:H&NCTF{haji_coke_you_win}
lcgp
from Crypto.Util.number import * |
一个套着LCG壳子的离散对数问题,需要先通过恢复参数倒推种子的方式来得到密文,可以通过LCG笔记 | Triode Field所讲述的方法来倒推参数得到seed,在此之后求离散对数即可得到flag:
from Crypto.Util.number import * |
可以得到flag:H&NCTF{7ecf4c8c-e6a5-45c7-b7de-2fecc31d8511}
数据处理
from Crypto.Util.number import bytes_to_long |
一个简单的离散对数问题,但是密文是经过换表的(本质上是一个置换),而且置换后表也只知道其中三个数字,所以可以知道这个置换如下: \[ \left(\begin{matrix} 0&1&2&3&4&5&6&7&8&9\\ 7&*&*&*&4&*&*&*&*&5 \end{matrix}\right) \] 那么需要通过爆破所有可能的置换来尝试还原得到flag:
from Crypto.Util.number import * |
可以得到flag:H&NCTF{cut_cut_rrioajtfijrwegeriogjiireigji}
为什么出题人的rsa总是ez
代码: #part 1
def pad(flag, bits=1024):
pad = os.urandom(bits//8 - len(flag))
return int.from_bytes(flag + pad, "big")
p = random_prime(2**1024)
q = random_prime(2**1024)
a = randint(0, 2**1024)
b = randint(0, 2**1024)
n = p * q
e = 0x10001
flag = b''
m = pad(flag)
assert m < n
c = pow(m, e, n)
print(f"c={c}")
print(f"n={n}")
print(f"h1={p + b * q}")
print(f"h2={a * p + q}")
# c=...
# n=...
# h1=...
# h2=...
#part 2
from Crypto.Util.number import *
from gmpy2 import *
a = random_prime()
b = random_prime()
g = random_prime()
h = 2*g*a*b+a+b
while not is_prime(h):
a = random_prime()
b = random_prime()
g = random_prime()
h = 2*g*a*b+a+b
N = 2*h*g+1
# e from part1's flag
flag=b''
c=pow(bytes_to_long(flag),e,N)
print(N)
print(g)
print(c)
#N=...
#g=...
#c=...
第一部分
给了\(h_1=ap+q\)和\(h_2=p+bq\),参考BLAHAJ - angstrom CTF 2024 - Connor M可以知道\(qh_1 + ph_2 - h_1h_2=0\),用如下脚本即可解出第一部分(参考了前面的文章说到的脚本):
load('https://gist.githubusercontent.com/Connor-McCartney/952583ecac836f843f50b785c7cb283d/raw/5718ebd8c9b4f9a549746094877a97e7796752eb/solvelinmod.py') |
可以得到: flag{e_is_xevaf-cityf-fisof-ketaf-metaf-disef-nuvaf-cysuf-dosuf-getuf-cysuf-dasix,bubbleBabble}

第二部分
给出质数\(g\),有\(h=2gab+a+b\),\(N=2hg+1\),显然这是Common Prime RSA,参考Common Prime RSA 笔记 | 独奏の小屋可以得到如下代码求解出flag: N = ...
g = ...
ct = ... # 密文
from sage.groups.generic import bsgs
e = 81733668723981020451323
h = (N - 1) // (2*g)
nbits = 2048
gamma = RR(g.bit_length() / nbits)
print("gamma:", gamma)
cbits = ceil(nbits * (0.5 - 2 * gamma))
M = (N - 1) // (2 * g)
u = M // (2 * g)
v = M - 2 * g * u
GF = Zmod(N)
x = GF.random_element()
y = x ^ (2 * g)
c = bsgs(y, y ^ u, (ZZ(2**(cbits-1)), ZZ(2**(cbits+1))))
ab = u - c
apb = v + 2 * g * c
P.<x> = ZZ[]
f = x ^ 2 - apb * x + ab
a = f.roots()
if a:
a, b = a[0][0], a[1][0]
p = 2 * g * a + 1
q = 2 * g * b + 1
assert p * q == N
phi = (p - 1) * (q - 1)
d = inverse_mod(e, phi)
m = pow(ct, d, N)
print(long_to_bytes(m))flag{I wish you success in your cryptography career}
ez-factor
from Crypto.Util.number import * |
有\(hint=kp+r\)(其中\(k\)是一个512位质数,\(r\)是一个248位质数),因为\(r\)很小,考虑构造多项式\(f=hint-x\)进行Coppersmith方法,使用参数\(X=2^{248},\beta=0.4,\varepsilon=0.01\)时可以求出一个小根\(r\),这个小根即为\(r\),从而可以得到\(p=(hint-r,N)\):
from Crypto.Util.number import * |
ez-factor-pro
这道题其实是赛后才看的
from Crypto.Util.number import * |
跟上一题差不多,就是\(r\)更大了,直接Coppersmith没办法搞出来,需要考虑爆破一下\(r\)的高位,按上一题来看的话爆破4位就行了,但是直接用sage自带的small_roots太慢了,考虑用flatter加速一下:
from Crypto.Util.number import * |
可以得到flag:

three vertical lines
这道题也是赛后做的,比赛的时候还没意识到之前做过一道类似的题
from Crypto.Util.number import * |
已知信息很少,只有一个\(3p^5+4q^5\)以及\(p,q\)都是质数,记\(3p^5+4q^5=r\),将该式置于模\(r\)下有: \[
3p^5+4q^5\equiv p^5+\frac{4}{3}q^5\equiv0\pmod{r}
\] 即: \[
p^5\equiv -\frac{4}{3}q^5\pmod{r}
\] 设整数\(a\in(0,r)\)满足\(a^5\equiv-\frac{4}{3}\pmod{r}\),那么有: \[
p^5\equiv(aq)^5\pmod{r}
\] 开根有: \[
p\equiv aq\pmod{r}
\] 即\(aq - kr=p\)(其中\(k\)为整数),那么可以构造出如下格: \[
\left(\begin{matrix}
1&a\\
0&-r
\end{matrix}\right)
\] 有如下关系: \[
(q,k)\left(\begin{matrix}
1&a\\
0&-r
\end{matrix}\right)=(q,p)
\] 通过格规约算法即可得到\(p,q\): from Crypto.Util.number import *
r = ...
c = ...
R.<x> = Zmod(r)[]
A = 4 * inverse(3, r) % r
f = x^5 + A
a = ZZ(f.roots()[0][0])
L = matrix(ZZ, [[1, a], [0, r]])
res = L.LLL()[0]
p = int(abs(res[0]))
q = int(abs(res[1]))
phi = (p - 1) * (q - 1)
d = inverse(65537, phi)
m = pow(c, d, p * q)
print(long_to_bytes(m))
Pwn
三步走战略
有个沙箱:
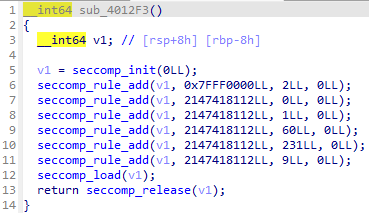
显然只允许使用open,write,read,又有输入部分:
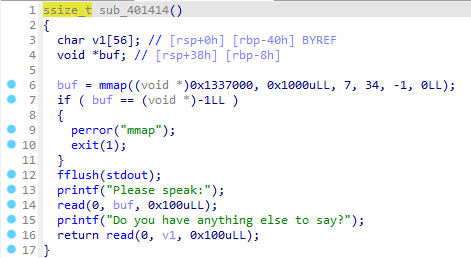
这里给buf分配了一个可读可写可执行而且很大的区间,所以我们可以向里面写入可执行代码,那么我们就可以向里面写入ORW的shellcode,之后通过栈溢出跳转执行那段shellcode:
from pwn import * |
shellcode
没有W的ORW,反编译可以看到:
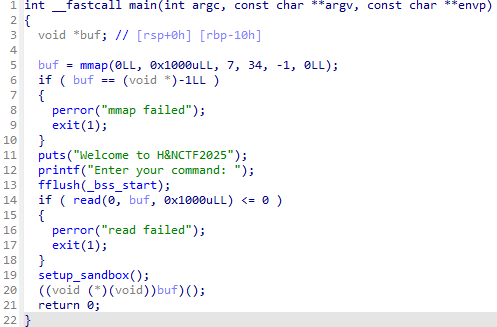
进入沙箱可以看到:
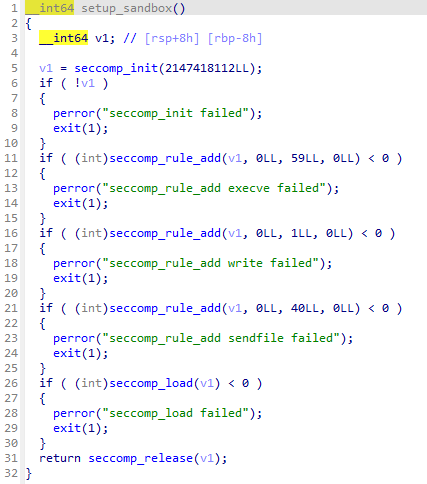
可以看到不能用execve和write还有sendfile,考虑通过测信道逐字符爆破flag,exp如下:
from pwn import * |
pdd助力
main函数反汇编如下:

可以见到第一部分随机数的种子只可能是0、1、2、3、4之间的一个减去44174237,我们可以选择0作为种子生成一串随机数,有20%的概率成功,而第二部分很显然固定了种子为8,这样的话就不用再去抽奖了,在这之后就会进入func函数:

明显存在栈溢出,而这个程序没有canary和PIE,所以可以直接打ret2libc,exp如下(成功率20%):
from pwn import * |
Web
Really_Ez_Rce
|
过滤了一堆命令的RCE,可以通过$(echo -n)输出空字符串的方式来绕过大部分命令限制,可以尝试通过遍历文件的方式来读取当前目录下的所有文件: for f in $(l$(echo -n)s); do c$(echo -n)a$(echo -n)t $f; done
index.php,因为/没有被过滤,所以l$(echo -n)s /查看根目录可以看到:

flag确实在根目录,因为cd没有被过滤,所以直接通过如下命令来遍历该目录并输出,因为根目录下只有flag.txt一个文件(其它均为目录),所以可以通过如下命令得到flag:
cd /; for f in $(l$(echo -n)s); do c$(echo -n)a$(echo -n)t $f; done |
传入cmd命令后可以得到flag:

