XYCTF 2025 部分题目Write Up

前言

去年明明说以后都不打这比赛的，今年还是来打了_(:3 」∠ )_

Crypto

Division

import random   
print('----Welcome to my division calc----')  
print('''  
menu:  
      [1]  Division calc      
      [2]  Get flag
''')  
while True:  
    choose = input(': >>> ')  
    if choose == '1':  
        try:  
            denominator = int(input('input the denominator: >>> '))  
        except:  
            print('INPUT NUMBERS')  
            continue  
        nominator = random.getrandbits(32)  
        if denominator == '0':  
            print('NO YOU DONT')  
            continue  
        else:  
            print(f'{nominator}//{denominator} = {nominator//denominator}')  
    elif choose == '2':  
        try:  
            ans = input('input the answer: >>> ')  
            rand1 = random.getrandbits(11000)  
            rand2 = random.getrandbits(10000)  
            correct_ans = rand1 // rand2  
            if correct_ans == int(ans):  
                print('WOW')  
                with open('flag', 'r') as f:  
                    print(f'Here is your flag: {f.read()}')  
            else:  
                print(f'NOPE, the correct answer is {correct_ans}')  
        except:  
            print('INPUT NUMBERS')  
    else:  
        print('Invalid choice')

MT19937随机数状态预测，分母全部传个1就可以直接得到生成的随机数，由此获取624个状态再预测就可以了：

from pwn import *  
from randcrack import *  
from tqdm import trange  
  
p = remote("ip", port)  
  
def get_state():  
    p.sendlineafter(b': >>> ', b'1')  
    p.sendlineafter(b'input the denominator: >>> ', b'1')  
    p.recvuntil(b'= ')  
    st = p.recvuntil(b'\n')  
    return int(st)  
  
rc = RandCrack()  
  
for _ in trange(624):  
    state = get_state()  
    rc.submit(state)  
  
rand1 = rc.predict_getrandbits(11000)  
rand2 = rc.predict_getrandbits(10000)  
  
p.sendlineafter(b': >>> ', b'2')  
p.sendlineafter(b'input the answer: >>> ', str(rand1 // rand2).encode())  
  
p.interactive()

from Crypto.Util.number import *  
from Crypto.Cipher import ChaCha20  
import hashlib  
from secret import flag  
  
  
class Complex:  
    def __init__(self, re, im):  
        self.re = re  
        self.im = im  
  
    def __mul__(self, c):  
        re_ = self.re * c.re - self.im * c.im  
        im_ = self.re * c.im + self.im * c.re  
        return Complex(re_, im_)  
  
    def __eq__(self, c):  
        return self.re == c.re and self.im == c.im  
  
    def __rshift__(self, m):  
        return Complex(self.re >> m, self.im >> m)  
  
    def __lshift__(self, m):  
        return Complex(self.re << m, self.im << m)  
  
    def __str__(self):  
        if self.im == 0:  
            return str(self.re)  
        elif self.re == 0:  
            if abs(self.im) == 1:  
                return f"{'-' if self.im < 0 else ''}i"  
            else:  
                return f"{self.im}i"  
        else:  
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"  
  
    def tolist(self):  
        return [self.re, self.im]  
  
  
def complex_pow(c, exp, n):  
    result = Complex(1, 0)  
    while exp > 0:  
        if exp & 1:  
            result = result * c  
            result.re = result.re % n  
            result.im = result.im % n  
        c = c * c  
        c.re = c.re % n  
        c.im = c.im % n  
        exp >>= 1  
    return result  
  
bits = 128  
p = getPrime(1024)  
q = getPrime(1024)  
n = p * q  
m = Complex(getRandomRange(1, n), getRandomRange(1, n))  
e = 3  
c = complex_pow(m, e, n)  
print(f"n = {n}")  
print(f"mh = {(m >> bits << bits).tolist()}")  
print(f"C = {c.tolist()}")  
print(f"enc = {ChaCha20.new(key=hashlib.sha256(str(m.re + m.im).encode()).digest(), nonce=b'Pr3d1ctmyxjj').encrypt(flag)}")  
  
'''  
n = ...  
mh = [..., ...]  
C = [..., ...]  
enc = ... 
'''

复数RSA，而且泄露了明文高位，对于明文$m$，可知：

$C=m^3=[Re(m)+i\cdot Im(m)]^3=[Re(m)^3 - 3Re(m)Im(m)^2] + i[3Re(m)^2Im(m) - Im(m)^3]$

在这里已知$Re(m)$以及$Im(m)$的高1920位，所以我们可以通过二元coppersmith来还原低位，在这里仅使用密文的实部（实际上用虚部也是可以的），可以构造得到多项式：

$f=(mh_0+x)^3-3(mh_0+x)(mh_1+y)^2-Re(C)$

上式中$mh_0,mh_1$对应题目给出数据中的mh[0],mh[1]，通过下述代码就可以得到flag了：

from Crypto.Util.number import *
from Crypto.Cipher import ChaCha20
import hashlib
import itertools

def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()
    R = f.base_ring()
    N = R.cardinality()
    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)
    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)
    B, monomials = G.coefficients_monomials()
    monomials = vector(monomials)
    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)
    B = B.dense_matrix().LLL()
    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)
    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots
    return []

n = ...
mh = [..., ...]
C = [..., ...]
enc = ...
bits = 128

R.<x, y> = Zmod(n)[]

re_m = mh[0] + x
im_m = mh[1] + y

f = re_m^3 - 3*re_m*im_m^2 - C[0]
a, b = small_roots(f, bounds=(2^bits, 2^bits), m=1, d=3)[0]

key = hashlib.sha256(str(mh[0] + mh[1] + ZZ(a) + ZZ(b)).encode()).digest()

cipher = ChaCha20.new(key=key, nonce=b'Pr3d1ctmyxjj')

plaintext = cipher.decrypt(enc)
print(plaintext.decode())

复复复复数

class ComComplex:  
    def __init__(self, value=[0,0,0,0]):  
        self.value = value  
    def __str__(self):  
        s = str(self.value[0])  
        for k,i in enumerate(self.value[1:]):  
            if i >= 0:  
                s += '+'  
            s += str(i) +'ijk'[k]  
        return s  
    def __add__(self,x):  
        return ComComplex([i+j for i,j in zip(self.value,x.value)])  
    def __mul__(self,x):  
        a = self.value[0]*x.value[0]-self.value[1]*x.value[1]-self.value[2]*x.value[2]-self.value[3]*x.value[3]  
        b = self.value[0]*x.value[1]+self.value[1]*x.value[0]+self.value[2]*x.value[3]-self.value[3]*x.value[2]  
        c = self.value[0]*x.value[2]-self.value[1]*x.value[3]+self.value[2]*x.value[0]+self.value[3]*x.value[1]  
        d = self.value[0]*x.value[3]+self.value[1]*x.value[2]-self.value[2]*x.value[1]+self.value[3]*x.value[0]  
        return ComComplex([a,b,c,d])  
    def __mod__(self,x):  
        return ComComplex([i % x for i in self.value])  
    def __pow__(self, x, n=None):  
        tmp = ComComplex(self.value)  
        a = ComComplex([1,0,0,0])  
        while x:  
            if x & 1:  
                a *= tmp  
            tmp *= tmp  
            if n:  
                a %= n  
                tmp %= n  
            x >>= 1  
        return a  
  
from Crypto.Util.number import *  
from secret import flag, hint  
  
p = getPrime(256)  
q = getPrime(256)  
r = getPrime(256)  
n = p * q * r  
  
P = getPrime(512)  
assert len(hint) == 20  
hints = ComComplex([bytes_to_long(hint[i:i+5]) for i in range(0,20,5)])  
keys = ComComplex([0, p, q, r])  
print('hint =',hints)  
print('gift =',hints*keys%P)  
print('P =',P)  
  
e = 65547  
m = ComComplex([bytes_to_long(flag[i:i+len(flag)//4+1]) for i in range(0,len(flag),len(flag)//4+1)])  
c = pow(m, e, n)  
print('n =', n)  
print('c =', c)

这个显然是一个四元数的RSA问题，那么我们首先需要分解出$n$，设hint为$h$，keys为$k$，gifts为$g$，则在模$P$的四元数下有：

$g=hk$

我们知道，四元数$a+bi+cj+dk$可以通过一个方阵等价表示：

$a+bi+cj+dk\leftrightarrow \left(\begin{matrix} a&b&c&d\\ -b&a&-d&c\\ -c&d&a&-b\\ -d&-c&b&a \end{matrix}\right)$

而四元数的乘法也可以等价地转换为矩阵的乘法，设$h$对应矩阵$H$，$k$对应矩阵$K$，$h$对应矩阵$G$，则上述计算可以等价于$G=HK$，这样的话我们就可以通过矩阵求逆得到$K$，从而得到$p,q,r$了（之后的操作都会将四元数处理为数组）：

# sage
h = [375413371936, 452903063925, 418564633198, 452841062207]
g = [8123312244520119413231609191866976836916616973013918670932199631084038015924368317077919454611785179950870055560079987034735836668109705445946887481003729, 20508867471664499348708768798854433383217801696267611753941328714877299161068885700412171, 22802458968832151777449744120185122420871929971817937643641589637402679927558503881707868, 40224499597522456323122179021760594618350780974297095023316834212332206526399536884102863]
P = 8123312244520119413231609191866976836916616973013918670932199631182724263362174895104545305364960781233690810077210539091362134310623408173268475389315109
n = 408713495380933615345467409596399184629824932933932227692519320046890365817329617301604051766392980053993030281090124694858194866782889226223493799859404283664530068697313752856923001112586828837146686963124061670340088332769524367

H = matrix(Zmod(P),
[[h[0], h[1], h[2], h[3]],
[-h[1], h[0], -h[3], h[2]],
[-h[2], h[3], h[0], -h[1]],
[-h[3], -h[2], h[1], h[0]]])

G = matrix(Zmod(P),
[[g[0], g[1], g[2], g[3]],
[-g[1], g[0], -g[3], g[2]],
[-g[2], g[3], g[0], -g[1]],
[-g[3], -g[2], g[1], g[0]]])

K = H^-1 * G
_, p, q, r = K[0]
assert ZZ(p) * ZZ(q) * ZZ(r) == n

p, q, r = ZZ(p), ZZ(q), ZZ(r)

在此之后就要求解四元数RSA了，已知四元数可以用一个四阶方阵来表示，那么我们从gr.group theory - maximal order of elements in GL(n,p) - MathOverflow中很容易知道在模$n=pqr$下的最大阶应为$\varphi=(p^4-1)(q^4-1)(r^4-1)$，但是在这里$(65547, \varphi)=9$，而且通过测试可以知道：

$(65547, p^4-1)=(65547, q^4-1)=(65547, r^4-1)=3$

我们猜测flag分块之后不可能大于$p,q,r$中任意一个，那么我们可以考虑尝试将该线性群的阶缩减为$\varphi/27$，此时通过普通的矩阵RSA就可以求得flag：

c = [212391106108596254648968182832931369624606731443797421732310126161911908195602305474921714075911012622738456373731638115041135121458776339519085497285769160263024788009541257401354037620169924991531279387552806754098200127027800103, 24398526281840329222660628769015610312084745844610670698920371305353888694519135578269023873988641161449924124665731242993290561874625654977013162008430854786349580090169988458393820787665342793716311005178101342140536536153873825, 45426319565874516841189981758358042952736832934179778483602503215353130229731883231784466068253520728052302138781204883495827539943655851877172681021818282251414044916889460602783324944030929987991059211909160860125047647337380125, 96704582331728201332157222706704482771142627223521415975953255983058954606417974983056516338287792260492498273014507582247155218239742778886055575426154960475637748339582574453542182586573424942835640846567809581805953259331957385]

C = matrix(Zmod(n),
[[c[0], c[1], c[2], c[3]],
[-c[1], c[0], -c[3], c[2]],
[-c[2], c[3], c[0], -c[1]],
[-c[3], -c[2], c[1], c[0]]])

e = 65547
phi = (p**4 - 1)*(q**4 - 1)*(r**4 - 1)//27

d = inverse(e, phi)
M = C^d

res = M[0]
flag = b""
for x in res:
    flag += long_to_bytes(ZZ(x))

print(flag)

reed

据说我的解法是非预期

import string  
import random  
from secret import flag  
  
assert flag.startswith('XYCTF{') and flag.endswith('}')  
flag = flag.rstrip('}').lstrip('XYCTF{')  
  
table = string.ascii_letters + string.digits  
assert all(i in table for i in flag)  
r = random.Random()  
  
class PRNG:  
    def __init__(self, seed):  
        self.a = 1145140  
        self.b = 19198100  
        random.seed(seed)  
  
    def next(self):  
        x = random.randint(self.a, self.b)  
        random.seed(x ** 2 + 1)  
        return x  
      
    def round(self, k):  
        for _ in range(k):  
            x = self.next()  
        return x  
  
def encrypt(msg, a, b):  
    c = [(a * table.index(m) + b) % 19198111 for m in msg]  
    return c  
  
seed = int(input('give me seed: '))  
prng = PRNG(seed)  
a = prng.round(r.randrange(2**16))  
b = prng.round(r.randrange(2**16))  
enc = encrypt(flag, a, b)  
print(enc)

有个仿射，而且我们知道字母表下标的范围，直接爆破参数$a$以及第一个字母就可以了（下面是种子为1的数据）：

import string  
import random  
from tqdm import trange  
from Crypto.Util.number import *  
  
table = string.ascii_letters + string.digits  
  
enc = [10021509, 10021509, 13396490, 1722743, 10021509, 13396490, 13616146, 16991127, 14667921, 6091782, 17765529, 12067342, 4542978, 16991127, 16216725, 3768576, 16991127, 15442323, 15442323, 4542978, 17765529, 14390548, 16216725, 1942399, 6091782, 7917959, 4542978, 11292940, 15442323, 10021509, 12622088, 10021509, 12622088, 5097724, 10021509, 2497145]  
  
for a in trange(114514, 19198100):  
    inva = inverse(a, 19198111)  
    for x in range(len(table)):  
        b = (enc[0] - a * x) % 19198111  
        if b > 1145140 and b < 19198100:  
            try:  
                flag = ''.join([table[(inva * (x - b)) % 19198111] for x in enc])  
                print(flag)  
                break  
            except:  
                pass

勒索病毒（复现）

给出一个exe，但是它的图标是：
Pasted image 20250410113323
看不出来是什么语言编译的，用DIE扫出来是C/C++：
Pasted image 20250410113519
拖进IDA里面看看，随便翻翻翻到：
Pasted image 20250410113656
有段代码提到了PyInstaller，初步判断是Python编译的，用pyinstxtractor解包可以得到task.pyc和res文件夹里的enc.txt和pub_key.txt，通过pycdc反编译得到如下代码（以下代码为反编译结果经过处理得到的)：

import re  
import base64  
import os  
import sys  
from gmssl import sm4  
from Crypto.Util.Padding import pad  
import binascii  
from random import shuffle, randrange  
  
N = 49 
p = 3  
q = 128  
d = 3  
assert q > (6 * d + 1) * p  
R.<x> = ZZ[]  
def generate_T(d1, d2):  
    assert N >= d1 + d2  
    s = [1] * d1 + [-1] * d2 + [0] * (N - d1 - d2)  
    shuffle(s)  
    return R(s)  
  
def invert_mod_prime(f, p):  
    Rp = R.change_ring(Integers(p)).quotient(x^N - 1)  
    return R(lift(1 / Rp(f)))  
  
def convolution(f, g):  
    return (f * g) % (x^N - 1)  
  
def lift_mod(f, q):  
    return R([((f[i] + q // 2) % q) - q // 2 for i in range(N)])  
  
def poly_mod(f, q):  
    return R([f[i] % q for i in range(N)])  
  
def invert_mod_pow2(f, q):  
    assert q.is_power_of(2)  
    g = invert_mod_prime(f, 2)  
    while True:  
        r = lift_mod(convolution(g, f), q)  
        if r == 1:  
            return g  
        g = lift_mod(convolution(g, 2 - r), q)  
  
def generate_message():  
    return R([randrange(p) - 1 for _ in range(N)])  
  
def generate_key():  
    while True:  
        try:  
            f = generate_T(d + 1, d)  
            g = generate_T(d, d)  
            Fp = poly_mod(invert_mod_prime(f, p), p)  
            Fq = poly_mod(invert_mod_pow2(f, q), q)  
            break  
        except:  
            continue  
    h = poly_mod(convolution(Fq, g), q)  
    return h, (f, g)  
  
def encrypt_message(m, h):  
    e = lift_mod(p * convolution(h, generate_T(d, d)) + m, q)  
    return e  
  
def save_ntru_keys():  
    h, secret = generate_key()  
    with open("pub_key.txt", "w") as f:  
        f.write(str(h))  
    m = generate_message()  
    with open("priv_key.txt", "w") as f:  
        f.write(str(m))  
    e = encrypt_message(m, h)  
    with open("enc.txt", "w") as f:  
        f.write(str(e))  
  
def terms(poly_str):  
    terms = []  
    pattern = r'([+-]?\s*x\^?\d*|[-+]?\s*\d+)'  
    matches = re.finditer(pattern, poly_str.replace(' ', ''))  
      
    for match in matches:  
        term = match.group()  
        if term == '+x' or term == 'x':  
            terms.append(1)  
        elif term == '-x':  
            terms.append(-1)  
        elif 'x^' in term:  
            coeff_part = term.split('x^')[0]  
            exponent = int(term.split('x^')[1])  
            if not coeff_part or coeff_part == '+':  
                coeff = 1  
            elif coeff_part == '-':  
                coeff = -1  
            else:  
                coeff = int(coeff_part)  
            terms.append(coeff * exponent)  
        elif 'x' in term:  
            coeff_part = term.split('x')[0]  
            if not coeff_part or coeff_part == '+':  
                terms.append(1)  
            elif coeff_part == '-':  
                terms.append(-1)  
            else:  
                terms.append(int(coeff_part))  
        else:  
            if term == '+1' or term == '1':  
                terms.append(0)  
                terms.append(-0)  
    return terms  
  
def gen_key(poly_terms):  
    binary = [0] * 128  
    for term in poly_terms:  
        exponent = abs(term)  
        if term > 0 and exponent <= 127:    
            binary[127 - exponent] = 1  
    binary_str = ''.join(map(str, binary))  
    hex_key = hex(int(binary_str, 2))[2:].upper().zfill(32)  
    return hex_key  
  
def read_polynomial_from_file(filename):  
    with open(filename, 'r') as file:  
        return file.read().strip()  
  
  
def sm4_encrypt(key, plaintext):  
    assert len(key) == 16, "SM4 key must be 16 bytes"  
    cipher = sm4.CryptSM4()  
    cipher.set_key(key, sm4.SM4_ENCRYPT)  
    padded_plaintext = pad(plaintext, 16)  
    return cipher.crypt_ecb(padded_plaintext)  
  
def sm4_encrypt_file(input_path, output_path, key):  
    with open(input_path, 'rb') as f:  
        plaintext = f.read()  
      
    ciphertext = sm4_encrypt(key, plaintext)  
      
    with open(output_path, 'wb') as f:  
        f.write(ciphertext)  
  
def resource_path(relative_path):  
    if getattr(sys, 'frozen', False):  
        base_path = sys._MEIPASS  
    else:  
        base_path = os.path.abspath(".")  
    return os.path.join(base_path, relative_path)  
  
def encrypt_directory(directory, sm4_key, extensions=[".txt"]):  
    if not os.path.exists(directory):  
        print(f"Directory does not exist: {directory}")  
        return  
    for root, _, files in os.walk(directory):  
        for file in files:  
            if any(file.endswith(ext) for ext in extensions):  
                input_path = os.path.join(root, file)  
                output_path = input_path + ".enc"  
                try:  
                    sm4_encrypt_file(input_path, output_path, sm4_key)  
                    os.remove(input_path)  
                    print(f"Encrypted: {input_path} -> {output_path}")  
                except Exception as e:  
                    print(f"Error encrypting {input_path}: {str(e)}")  
  
def main():  
    try:  
        save_ntru_keys()  
        poly_str = read_polynomial_from_file("priv_key.txt")  
        poly_terms = terms(poly_str)  
        sm4_key = binascii.unhexlify(poly_terms)  
        user_name = os.getlogin()  
        target_dir = os.path.join("C:\\Users", user_name, "Desktop", "test_files")  
          
        if not os.path.exists(target_dir):  
            os.makedirs(target_dir, exist_ok=True)  
            print(f"Created directory: {target_dir}")  
            return  
            txt_files = [f for f in os.listdir(target_dir)   
                    if f.endswith('.txt') and os.path.isfile(os.path.join(target_dir, f))]  
          
        if not txt_files:  
            print("No .txt files found in directory")  
            return  
            for txt_file in txt_files:  
            file_path = os.path.join(target_dir, txt_file)  
            try:  
                with open(file_path, 'rb') as f:  
                    test_data = f.read()  
                  
                ciphertext = sm4_encrypt(sm4_key, test_data)  
                encrypted_path = file_path + '.enc'  
                with open(encrypted_path, 'wb') as f:  
                f.write(ciphertext)  
            except Exception as e:  
                print(f"Error processing {txt_file}: {str(e)}")  
                  
    except Exception as e:  
        print(f"Fatal error: {str(e)}")  
  
if __name__ == "__main__":  
    main()

可以看到上述代码生成一个随机多项式$m(x)$，并通过terms（以及反编译出来的代码中没有使用到的gen_key）来讲多项式转换为SM4的密钥对flag进行加密，之后使用NTRU加密多项式$m(x)$，最后将NTRU的公钥写入pub_key.txt，将NTRU的密文写入enc.txt，NTRU相关可以参考这篇博客：NTRU | Triode Field，通过如下代码就可以求解出flag：

from Crypto.Util.number import *
from Crypto.Util.Padding import unpad
import re
import binascii
from gmssl import sm4

def terms(poly_str):
    terms = []
    pattern = r'([+-]?\s*x\^?\d*|[-+]?\s*\d+)'
    matches = re.finditer(pattern, poly_str.replace(' ', ''))
    for match in matches:
        term = match.group()
        if term == '+x' or term == 'x':
            terms.append(1)
        elif term == '-x':
            terms.append(-1)
        elif 'x^' in term:
            coeff_part = term.split('x^')[0]
            exponent = int(term.split('x^')[1])
            if not coeff_part or coeff_part == '+':
                coeff = 1
            elif coeff_part == '-':
                coeff = -1
            else:
                coeff = int(coeff_part)
            terms.append(coeff * exponent)
        elif 'x' in term:
            coeff_part = term.split('x')[0]
            if not coeff_part or coeff_part == '+':
                terms.append(1)
            elif coeff_part == '-':
                terms.append(-1)
            else:
                terms.append(int(coeff_part))
        else:
            if term == '+1' or term == '1':
                terms.append(0)
                terms.append(-0)
    return terms

def gen_key(poly_terms):
    binary = [0] * 128
    for term in poly_terms:
        exponent = abs(term)
        if term > 0 and exponent <= 127:
            binary[127 - exponent] = 1
    binary_str = ''.join(map(str, binary))
    hex_key = hex(int(binary_str, 2))[2:].upper().zfill(32)
    return hex_key

N = 49
p = 3
q = 128  
d = 3

_R = PolynomialRing(ZZ, 'x')
R = _R.quotient(x^N - 1, 'x')

_Rp = PolynomialRing(Zmod(p), 'x')
Rp = _Rp.quotient(x^N - 1, 'x')

_Rq = PolynomialRing(Zmod(q), 'x')
Rq = _Rq.quotient(x^N - 1, 'x')

def center_lift(Rm, R, f):
    modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
    l = [ZZ(x) if x <= modulo // 2 else ZZ(x) - modulo for x in list(f)]
    return R(l)

def inv(Rm, f):
    return Rm(f).inverse()

h = R("...")
e = R("...")

L = matrix(ZZ, 2*N, 2*N)

h_coeff = [ZZ(x) for x in list(h)]
for i in range(N):
    L[i, i] = 1
    L[N + i, N + i] = q
    for j in range(N):
        L[i, N + j] = h_coeff[(j - i) % N]\

res = L.BKZ()[0]

v = list(res[:N])
f = R([ZZ(x) for x in v])
Fp = Rp(list(f)).inverse()
a = center_lift(Rq, R, Rq(list(f * e)))
m = center_lift(Rp, R, Rp(list(Fp * a)))

print(m)
poly_terms = terms(str(m))
key = gen_key(poly_terms)
sm4_key = binascii.unhexlify(key)
print(sm4_key.hex())

sm4 = sm4.CryptSM4(sm4_key)
sm4.set_key(sm4_key, gmssl.sm4.SM4_DECRYPT)

ct = bytes.fromhex("bf0cb5cc6bea6146e9c1f109df953a57daa416d38a8ffba6438e7e599613e01f3b9a53dace4ccd55cd3e55ef88e0b835")
pt = sm4.crypt_ecb(ct)
print(unpad(pt, 16))

事实上，我们可以发现，在enc.txt中除了$e$之外还有一个多出来的多项式：

-x^48 - x^46 + x^45 + x^43 - x^42 + x^41 + x^40 + x^36 - x^35 + x^34 - x^33 + x^32 - x^30 + x^29 - x^28 - x^27 - x^26 - x^25 - x^23 - x^22 + x^21 + x^20 + x^19 + x^18 - x^17 - x^16 - x^15 - x^14 - x^12 + x^9 - x^7 - x^6 - x^5 - x^4 + x^3 - x + 1

这个多项式实际上就是NTRU加密一步使用的明文，也就是最后被用于转换为SM4的密钥的多项式.

choice（复现）

from Crypto.Util.number import bytes_to_long  
from random import Random  
from secret import flag  
  
assert flag.startswith(b'XYCTF{') and flag.endswith(b'}')  
flag = flag[6:-1]  
  
msg = bytes_to_long(flag)  
rand = Random()  
test = bytes([i for i in range(255, -1, -1)])  
open('output.py', 'w').write(f'enc = {msg ^ rand.getrandbits(msg.bit_length())}\nr = {[rand.choice(test) for _ in range(2496)]}')

给了上面的代码还有random.py，跟Python库里面的random.py差距挺大的，但是据出题人的说法修改的是第246行，对应的是_randbelow_with_getrandbits函数，原本的这个函数实现如下：

def _randbelow_with_getrandbits(self, n):  
    "Return a random int in the range [0,n).  Defined for n > 0."  
  
    getrandbits = self.getrandbits  
    k = n.bit_length()  # don't use (n-1) here because n can be 1  
    r = getrandbits(k)  # 0 <= r < 2**k  
    while r >= n:  
        r = getrandbits(k)  
    return r

修改后是这样的：

def _randbelow_with_getrandbits(self, n):  
    "Return a random int in the range [0,n).  Defined for n > 0."  
  
    getrandbits = self.getrandbits  
    k = n.bit_length() - 1  
    r = getrandbits(k)  # 0 <= r < 2**k  
    while r >= n:  
        r = getrandbits(k)  
    return r

其实就是将k = n.bit_length()修改成了k = n.bit_length() - 1，再看到题目主要使用的choice函数实现如下：

def choice(self, seq):  
    """Choose a random element from a non-empty sequence."""  
  
    # As an accommodation for NumPy, we don't use "if not seq"  
    # because bool(numpy.array()) raises a ValueError.    if not len(seq):  
        raise IndexError('Cannot choose from an empty sequence')  
    return seq[self._randbelow(len(seq))]

如果用原来的代码的话在进行rand.choice(test)的时候_randbelow_with_getrandbits就会生成9-bits的随机数，若大于等于256就会重新选取，这样的话得到的状态是不连续的，就没有办法恢复状态并倒推了，所以将k = n.bit_length()修改成了k = n.bit_length() - 1就可以避免这种情况，恢复状态的话GitHub上这个项目就可以做到，通过下述代码就可以恢复状态并实现倒推：

import sys
sys.path.append('MT19937-Symbolic-Execution-and-Solver/source')

from MT19937 import MT19937
from Crypto.Util.number import *

enc = 5042764371819053176884777909105310461303359296255297

r = [...]
r = [255 - x for x in r]

rng_clone = MT19937(state_from_data = (r, 8))

length = enc.bit_length()

rng_clone.reverse_states(length//32+1) # 括号内参数是要倒推的状态数

恢复状态之后则需要通过手写getrandbits函数来得到（那个项目并没有实现这个功能），根据random库中getrandbits的规则实现getrandbits如下：

def getrandbits(n):
    out = 0
    offset = 0
    while n > 32:
        out = rng_clone() << offset | out
        n -= 32
        offset += 32
    out = rng_clone() >> (32 - n) << offset | out
    return out

最终可以直接恢复出flag：

mask = getrandbits(length + 3) # 需要测试，因为不知道原来的位数是多少，只知道密文的位数
pt = enc ^^ mask 

print(long_to_bytes(pt))

prng_xxxx（待复现）

from Crypto.Cipher import AES  
from Crypto.Util.Padding import pad  
from hashlib import md5  
from secret import flag, b, seed  
  
class LCG:  
    def __init__(self, seed, a, b):  
        self.seed = seed  
        self.a = a  
        self.b = b  
        self.m = 2**128  
  
    def next(self):  
        self.seed = (self.seed * self.a + self.b) % self.m  
        return (self.seed >> 64) ^ (self.seed % 2**64)  
  
class lfsr:  
    # 我被裁了/(ㄒoㄒ)/~~  
    pass  
  
a = 47026247687942121848144207491837523525  
assert b < 2**128 and seed < 2**128  
lcg = LCG(seed, a, b)  
print([lcg.next() for _ in [0] * 64])  
print(AES.new(key=md5(str(seed).encode()).digest(), mode=AES.MODE_ECB).encrypt(pad(flag, 16)))

参考论文：View of Practical seed-recovery for the PCG Pseudo-Random Number Generator

~~听说预期解的exp也要跑一个小时，有闲情雅致再复现~~

Misc

签个到吧

经典Brainfuck，美化代码如下：

>+++++++++++++++++
[<++++++>-+-+-+-]
<
[-]
>++++++++++++
[<+++++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++
[<+++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++
[<+++>-+-+-+-]
<
[-]
>+++++++++++++++++
[<+++>-+-+-+-]
<
[-]
>++++++++++++
[<+++++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>++++++++
[<++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++
[<++++>-+-+-+-]
<
[-]
>++++++++
[<++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++++++
[<++++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>++++++++++++
[<+++++++>-+-+-+-]
<
[-]
>++++++++++
[<+++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]
>++++++++++
[<+++++>-+-+-+-]
<
[-]
>++++++++
[<++++++>-+-+-+-]
<
[-]
>++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++
[<+++>-+-+-+-]
<
[-]
>+++++++++++
[<++++++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++
[<++>-+-+-+-]
<
[-]
>++++++++
[<++++++>-+-+-+-]
<
[-]
>+++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]
>+++++++
[<+++++++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++++++
[<++++>-+-+-+-]
<
[-]
>+++++++++++
[<+++>-+-+-+-]
<
[-]
>+++++++++++++++++++++++++
[<+++++>-+-+-+-]
<
[-]

可以知道这里在地址为0处写入数据之后会将它擦除，所以可以在擦除之前将地址为0的数据打印出来，修改代码如下：

>+++++++++++++++++
[<++++++>-+-+-+-]
<.
[-]
>++++++++++++
[<+++++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++
[<+++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++
[<+++>-+-+-+-]
<.
[-]
>+++++++++++++++++
[<+++>-+-+-+-]
<.
[-]
>++++++++++++
[<+++++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>++++++++
[<++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++
[<++++>-+-+-+-]
<.
[-]
>++++++++
[<++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++++++
[<++++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>++++++++++++
[<+++++++>-+-+-+-]
<.
[-]
>++++++++++
[<+++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]
>++++++++++
[<+++++>-+-+-+-]
<.
[-]
>++++++++
[<++++++>-+-+-+-]
<.
[-]
>++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++
[<+>-+-+-+-]
<.
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++
[<+++>-+-+-+-]
<.
[-]
>+++++++++++
[<++++++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++++++++++++++++++++++++++
[<++>-+-+-+-]
<.
[-]
>++++++++
[<++++++>-+-+-+-]
<.
[-]
>+++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]
>+++++++
[<+++++++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++++++
[<++++>-+-+-+-]
<.
[-]
>+++++++++++
[<+++>-+-+-+-]
<.
[-]
>+++++++++++++++++++++++++
[<+++++>-+-+-+-]
<.
[-]

XGCTF

题目描述：
2024年CTFshow举办了一场名为“西瓜杯”的比赛（XGCTF）。其中LamentXU在出题的时候，从某场比赛拉了道原题下来改了改，结果传文件的时候传错了传成原题了。因为这件事LamentXU的损友dragonkeep在他之前的博客上的原题wp上加了一段flag来嘲笑LamentXU。请你找到XGCTF中唯一由LamentXU出的题，并找出这题对应的原题，接着找到dragonkeep师傅的博客，并从博客上讲解该题的博文中找到flag。（hint：dragonkeep师傅因为比较穷买不起域名，因此他博客的域名在dragonkeep的基础上多了个字母）

从题目描述中可以整理出三条线索：

flag在dragonkeep的博客里
这道题的flag所在的位置与XGCTF的一道原题有关
相关题目在XGCTF中标注的出题人为LamentXU

首先可以找到dragonkeep的博客为：https://dragonkeeep.top，可以看到这个师傅主攻的方向应该是web，所以可以大致将范围缩小到XGCTF的web题，直接到[XGCTF的复现平台](https://ctf.show/challenges)中可以找到唯一一道由LamentXU提供的题目：
Pasted image 20250404173308
关键词应该是polluted，回到dragonkeep的博客中可以发现一篇文章跟polluted有关：CISCN华东南WEB-Polluted | Dragonkeep，在里面找一圈没找到flag，看看是不是在网页HTML源代码的注释里面，查看网页源代码可以找到：

<!--Congratulations! You've got the flag:ZmxhZ3sxdF9JM190M0Vfc0BNZV9DaEFsMWVOZ2VfYVRfYTFMX1AxZUBzZV9mT3JnMXZlX01lfQ== -->

base64解码就是flag了.

会飞的雷克萨斯

在比赛群里给出flag的格式为flag{xx省xx市xx县xxx路xxxxxx内}，一个x对应一个字

OSINT，给出一张图片：
ab3f53c6b3d2cfd23674a0c6e277d895

直接搜索题目名字可以发现这是今年新年小孩玩炮仗炸化粪池把车炸飞的其中一个当事人在事发后改的网名，大多数新闻都显示发生的位置是四川省内江市资中县春岚北路，但是没有给出具体小区名，这个时候需要结合图片，注意到有一间叫唯曼医疗美容的店，百度地图搜索可以看到唯一结果：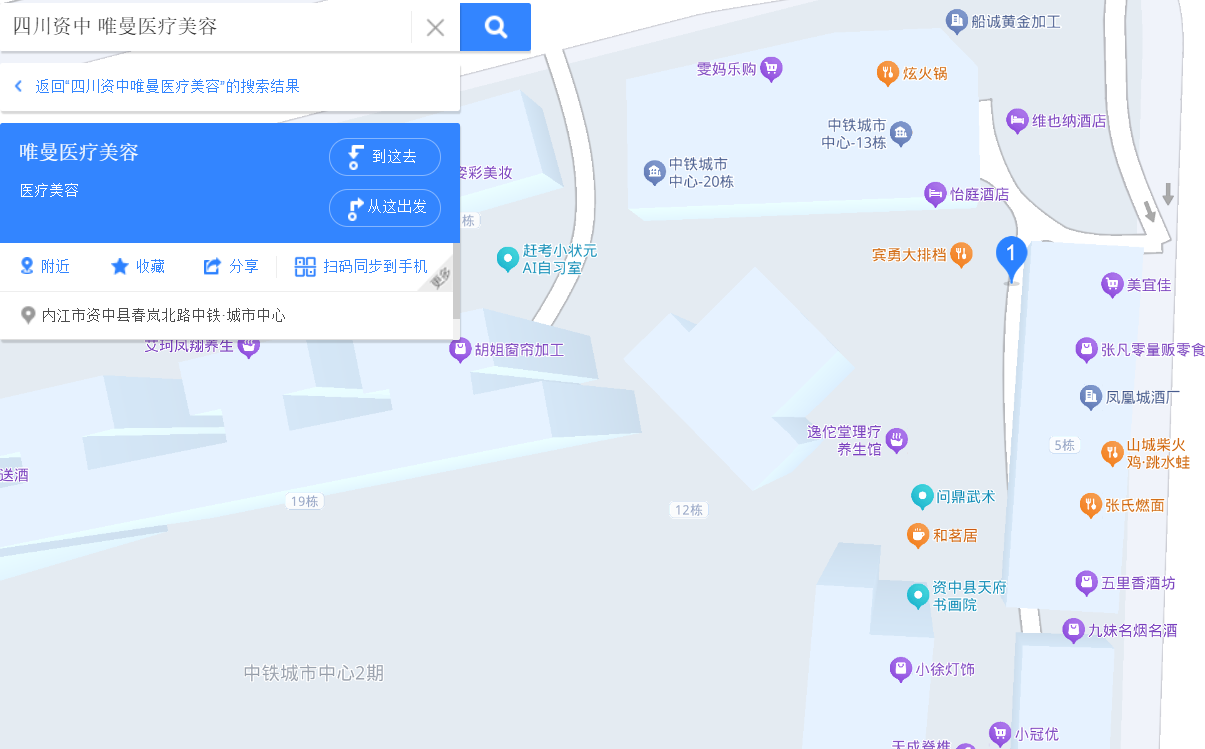
Pasted image 20250406232555
可以知道事发地是在中铁城市中心内，所以flag就是flag{四川省内江市资中县春岚北路中铁城市中心内}

曼波曼波曼波

给了个smn.txt，打开发现是倒过来的Base64，解码之后是张图片：
smn
附件里面还有个二维码，但是是假的flag，不用管，010可以看到上面图片的末尾有段zip，拉出来之后解压发现有一张图片，一个压缩包还有一个txt，txt里面是对压缩包密码的提示：

密码是什么来着，有点记不清了，呜呜呜呜
好像是什么比赛名字加年份

不用想都知道是XYCTF2025，解压发现一张跟外面的图片看上去一模一样的图片，且尺寸也是一致的，考虑盲水印，解盲水印可以看到：
out
肉眼识别可以得到flag为XYCTF{easy_yin_xie_dfbfuj877}

Reverse

WARMUP

vbs逆向，用记事本打开并将开头的Execute改成wscript.echo，然后在命令行用cscript运行可以得到源码：

MsgBox "Dear CTFER. Have fun in XYCTF 2025!"
flag = InputBox("Enter the FLAG:", "XYCTF")
wefbuwiue = "90df4407ee093d309098d85a42be57a2979f1e51463a31e8d15e2fac4e84ea0df622a55c4ddfb535ef3e51e8b2528b826d5347e165912e99118333151273cc3fa8b2b3b413cf2bdb1e8c9c52865efc095a8dd89b3b3cfbb200bbadbf4a6cd4"
qwfe = "rc4key"

Function RunRC(sMessage, strKey)
    Dim kLen, i, j, temp, pos, outHex
    Dim s(255), k(255)

    kLen = Len(strKey)
    For i = 0 To 255
        s(i) = i
        k(i) = Asc(Mid(strKey, (i Mod kLen) + 1, 1)) 
    Next

    j = 0
    For i = 0 To 255
        j = (j + s(i) + k(i)) Mod 256
        temp = s(i)
        s(i) = s(j)
        s(j) = temp
    Next

    i = 0 : j = 0 : outHex = ""
    For pos = 1 To Len(sMessage)
        i = (i + 1) Mod 256
        j = (j + s(i)) Mod 256
        temp = s(i)
        s(i) = s(j)
        s(j) = temp

        Dim plainChar, cipherByte
        plainChar = Asc(Mid(sMessage, pos, 1)) 
        cipherByte = s((s(i) + s(j)) Mod 256) Xor plainChar
        outHex = outHex & Right("0" & Hex(cipherByte), 2)
    Next

    RunRC = outHex
End Function

If LCase(RunRC(flag, qwfe)) = LCase(wefbuwiue) Then
    MsgBox "Congratulations! Correct FLAG!"
Else
    MsgBox "Wrong flag."
End If

就是RC4加密，密钥为rc4key，用CyberChef解密就可以得到flag了.