NTRU
参考资料:An Introduction to Mathematical Cryptography | SpringerLink
前置知识
格
与格相关的前置知识在这篇博客里面都有提及
卷积多项式环
对于一个整数\(N\),秩为\(N\)的卷积多项式环即为如下商环: \[ R=\frac{\mathbb{Z}[x]}{(x^{N}-1)} \] 类似的我们也可以定义出模\(q\)的卷积多项式环为如下商环: \[ R_q=\frac{(\mathbb{Z}/q\mathbb{Z})[x]}{(x^{N}-1)} \] 可以知道卷积多项式环中每一个多项式\(a(x)\)都有唯一的表示(在这之后,我们默认卷积多项式环内的多项式都是如下表示): \[ a(x)=a_0+a_1x+a_2x^2+\cdots+a_{N-1}x^{N-1} \] 其中\(a_0,a_1,\cdots,a_{N-1}\in \mathbb{Z}\)(或者\(\mathbb{Z}/q\mathbb{Z}\),这取决于这个卷积多项式环是一般的卷积多项式环还是模\(q\)的卷积多项式环) 卷积多项式环是NTRU密码体系的基础。
center-lift
对于\(R_q\)上一个多项式\(a(x)\),\(a(x)\)到\(R\)上的center-lift即为一个多项式\(a'(x)\)满足: \[
a'(x)\equiv a(x)\pmod{q}
\] 其中\(a'(x)\)的系数\(a_i'\in(-\frac{q}{2},-\frac{q}{2}]\). 对于一个多项式,要获得其center-lift有如下算法: \[
a_i'=
\begin{cases}
a_i&,0\le a_i\le\frac{q}{2}\\
a_i-q&,\frac{q}{2}< a_i< q
\end{cases}
\] center-lift可以通过如下代码实现: def center_lift(Rm, R, f):
modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
l = [ZZ(x) if x <= modulo // 2 else ZZ(x) - modulo for x in list(f)]
return R(l)
三元多项式(ternary polynomial)
对于卷积多项式环\(R=\frac{\mathbb{Z}[x]}{(x^{N}-1)}\),对于任意正数\(d_1,d_2\),若多项式\(a(x)\in R\)满足以下条件:
- \(a(x)\)中有\(d_1\)个系数为\(1\);
- \(a(x)\)中有\(d_2\)个系数为\(-1\);
- \(a(x)\)中其余系数均为\(0\).
则称这个多项式为一个三元多项式(ternary polynomial,或称trinary polynomial),对于一个卷积多项式环\(R\),其上的所有三元多项式的集合记为: \[ \mathcal{T}(d_1,d_2)=\left\{a(x)\in R| a(x)\text{ is a ternary polynomial}\right\} \]
NTRU算法细节
取整数\(N\ge1\)以及两个模数\(p,q\)(其中\(N\)为质数,且\(N\)与\(q\)互质,\(p\)与\(q\)互质),得到如下三个卷积多项式环: \[
R=\frac{\mathbb{Z}[x]}{(x^{N}-1)},\quad R_p=\frac{(\mathbb{Z}/p\mathbb{Z})[x]}{(x^{N}-1)},\quad R_q=\frac{(\mathbb{Z}/q\mathbb{Z})[x]}{(x^{N}-1)}
\] 在此我们将消息传递的双方分别称为Alice和Bob,Alice选取公共参数\((N,p,q,d)\)(\(d\)也是个整数,公共参数的选择应满足\(q>(6d+1)p\)),并在\(R\)上随机选取三元多项式\(f(x)\in\mathcal{T}(d+1,d)\)以及\(g(x)\in\mathcal{T}(d,d)\),计算: \[
\begin{aligned}
F_p\equiv f^{-1}\pmod{p}\\
F_q\equiv f^{-1}\pmod{q}
\end{aligned}
\] 这样就可以得到一个\(R_p\)上的多项式\(F_p\)以及一个\(R_q\)上的多项式\(F_q\),在此之后Alice在\(R_q\)上计算: \[
h(x)=F_q(x)\star g(x)
\] 在这里“\(\star\)”表示卷积多项式环上多项式的乘法,对于两个卷积多项式环\(R\)上的多项式\(a(x),b(x)\),其乘积定义如下: \[
a(x)\star b(x)=c(x),\quad c_k=\sum_{i+j\equiv k\pmod{N}}{a_{i}b_{j}}
\] 由此计算出的多项式\(h(x)\)即为公钥,前面生成的\((f,F_p)\)就是私钥(实际上私钥只需要\(f\),Alice可以通过\(f\)来计算出\(F_p\))。 在此之后Bob需要通过公钥\(h(x)\)来加密明文\(m(x)\)(其中明文\(m(x)\in R\),而且其中系数\(m_i\)满足\(-\frac{p}{2}<m_i\le \frac{p}{2}\),实际上\(m(x)\)就是\(R_p\)上某个多项式的center-lift),Bob先选取一个随机三元多项式\(r(x)\in\mathcal{T}(d,d)\),计算: \[
e(x)\equiv ph(x)\star r(x)+m(x)\pmod{q}
\] 得到的多项式\(e(x)\)就是Bob的密文,Alice得到Bob发送的密文之后要进行解密,则需先在\(R_q\)上计算: \[
a(x)\equiv f(x)\star e(x)\pmod{q}
\] 然后得到\(a(x)\)的center-lift,然后再在\(R_p\)中计算: \[
b(x)\equiv F_p(x)\star a(x)\pmod{p}
\] 这样得到的\(R_p\)上的多项式\(b(x)\)就是明文\(m(x)\). NTRU大致流程如下图所示(在参考资料里截的): 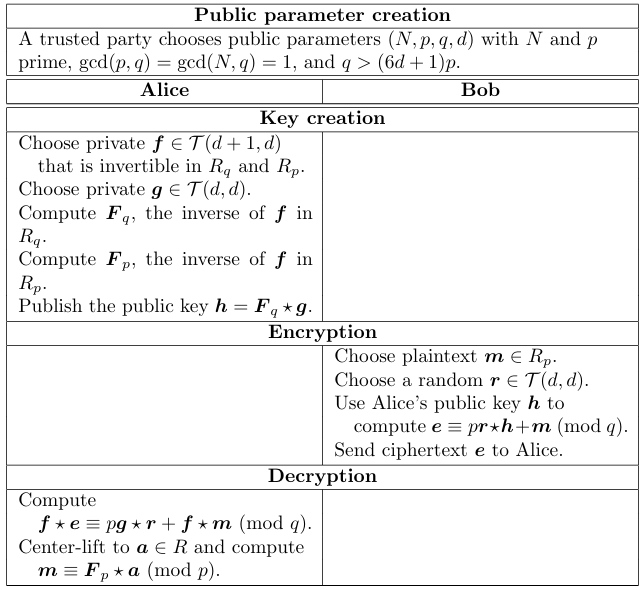
NTRU的实现
在这里通过sage实现参考资料中的一个例子(Example 7.53): 取\((N, p, q, d) = (7, 3, 41, 2)\),显然有\((6d+1)p=39<q\),而且\((p,q)=1,(N,q)=1\),符合参数选择的条件,那么可以通过如下代码构造出三个卷积多项式环: _R = PolynomialRing(ZZ, 'x')
R = _R.quotient(x^N - 1, 'x')
_Rp = PolynomialRing(Zmod(p), 'x')
Rp = _Rp.quotient(x^N - 1, 'x')
_Rq = PolynomialRing(Zmod(q), 'x')
Rq = _Rq.quotient(x^N - 1, 'x')def T(R, N, d1, d2):
from random import shuffle
coef = [1] * d1 + [-1] * d2 + [0] * (N - d1 - d2)
shuffle(coef)
return R(coef)def inv(Rm, f):
return Rm(list(f)).inverse()invertmodpowerof2的算法,经过修改得到了下面的版本: def invertmodpowerof2(Rm, R, f):
modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
assert modulo.is_power_of(2)
_R2 = PolynomialRing(Zmod(2), 'x')
R2 = _R2.quotient(x^N - 1, 'x')
g = R2(list(f)).inverse()
while True:
r = center_lift(Rm, R, Rm(list(f * g)))
if r == 1:
return g
g = center_lift(Rm, R, Rm(list(g * (2 - r))))Fp = inv(Rp, f)
Fq = inv(Rq, f)h = Fq * Rq(list(g))
e = Rq(list(p*r*h + m))在\(R_q\)上计算\(e(x)\equiv pr(x)\star h(x)+m(x)\pmod{q}\),得到密文: \[
e(x)=31 x^{6} + 19 x^{5} + 4 x^{4} + 2 x^{3} + 40 x^{2} + 3 x + 25
\] 参数选取以及加密全流程代码如下: (N, p, q, d) = (7, 3, 41, 2)
_R = PolynomialRing(ZZ, 'x')
R = _R.quotient(x^N - 1, 'x')
_Rp = PolynomialRing(Zmod(p), 'x')
Rp = _Rp.quotient(x^N - 1, 'x')
_Rq = PolynomialRing(Zmod(q), 'x')
Rq = _Rq.quotient(x^N - 1, 'x')
def T(R, N, d1, d2):
from random import shuffle
coef = [1] * d1 + [-1] * d2 + [0] * (N - d1 - d2)
shuffle(coef)
return R(coef)
def center_lift(Rm, R, f):
modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
l = [ZZ(x) if x <= modulo // 2 else ZZ(x) - modulo for x in list(f)]
return R(l)
def inv(Rm, f):
return Rm(f).inverse()
def invertmodpowerof2(Rm, R, f):
modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
assert modulo.is_power_of(2)
_R2 = PolynomialRing(Zmod(2), 'x')
R2 = _R2.quotient(x^N - 1, 'x')
g = R2(list(f)).inverse()
while True:
r = center_lift(Rm, R, Rm(list(f * g)))
if r == 1:
return g
g = center_lift(Rm, R, Rm(list(g * (2 - r))))
# f = T(R, N, d + 1, d)
f = R("x^6 - x^4 + x^3 + x^2 - 1") # private key
# g = T(R, N, d, d)
g = R("x^6 + x^4 - x^2 - x")
Fp = inv(Rp, f)
Fq = inv(Rq, f)
h = Fq * Rq(list(g)) # public key
m = R("-x^5+x^3+x^2-x+1")
# r = T(R, N, d, d)
r = R("x^6-x^5+x-1")
e = Rq(list(p*r*h + m))a = center_lift(Rq, R, Rq(list(f * e)))
然后在\(R_p\)上计算\(F_p\star a(x)\)并获取其center-lift得到\(b(x)\): b = center_lift(Rp, R, Rp(list(Fp * a)))
a = center_lift(Rq, R, Rq(list(f * e)))
b = center_lift(Rp, R, Rp(list(Fp * a)))
NTRU的格攻击
回到公钥计算这一步,我们需要在\(R_q\)上计算\(h(x)=F_q(x)\star g(x)\),两边乘上\(f(x)\)可以得到: \[
f(x)\star h(x)\equiv g(x)\pmod{q}
\] 与对数的处理方法类似的,可以将上式变为: \[
f(x)\star h(x)=g(x)+q\cdot u(x)
\] 其中\(u(x)\in R\),我们想要的是私钥\(f(x)\),那么可以构造出如下方程: \[
(f(x),-u(x))
\left(\begin{matrix}
1&h(x)\\
0&q
\end{matrix}\right)=
(f(x),g(x))\tag{1}
\] 但是直接对多项式矩阵进行规约应该是不太可能的,那么需要找到一种方法来将多项式矩阵转换为一般的矩阵,先前提到对于两个卷积多项式环\(R\)上的多项式\(a(x),b(x)\),其乘积定义为: \[
a(x)\star b(x)=c(x),\quad c_k=\sum_{i+j\equiv k\pmod{N}}{a_{i}b_{j}}
\] 显然有: \[
c_k=(a_0,a_1,\cdots,a_{N-1})\cdot(b_{k\mod{N}},b_{k-1\mod{N}},\cdots,b_{k-N+1\mod{N}})^T
\] 那么可以得到: \[
(c_0,c_1,\cdots, c_{N-1})=(a_0,a_1,\cdots,a_{N-1})
\left(\begin{matrix}
b_0&b_1&\cdots&b_{N-1}\\
b_{N-1}&b_0&\cdots&b_{N-2}\\
\vdots&\vdots&&\vdots\\
b_{1}&b_{2}&\cdots&b_{0}
\end{matrix}\right)
\] 实际上等式右边的矩阵是\(b(x)\)的系数的循环排列,这样我们就可以将矩阵内的\(h(x)\)转换为一个\(n\times n\)的矩阵: \[
H=\left(\begin{matrix}
h_0&h_1&\cdots&h_{N-1}\\
h_{N-1}&h_0&\cdots&h_{N-2}\\
\vdots&\vdots&&\vdots\\
h_{1}&h_{2}&\cdots&h_{0}
\end{matrix}\right)
\] 同理,由于\(1\)以及\(q\)也可以看作是仅有常数项不为\(0\)的多项式,所以可以将它们分别转换为单位矩阵\(I\)以及\(q\)倍的单位矩阵\(qI\),而行向量内的多项式\(f(x)\)可以转换为其对应的系数向量\(\pmb{f}=(f_0,f_1,\cdots,f_{N-1})\),同理\(u(x),g(x)\)也可以转换为对应的系数向量\(\pmb{u}\)以及\(\pmb{g}\),那么我们就可以得到方程\((1)\)的等价表示: \[
(\pmb{f},-\pmb{u})
\left(\begin{matrix}
I&H\\
0&qI
\end{matrix}\right)=(\pmb{f},\pmb{g})
\] 其中\(2N\times2N\)矩阵\(\left(\begin{matrix}I&H\\0&qI\end{matrix}\right)\)所确定的格被称为NTRU格(NTRU Lattice)一般记为\(\mathcal{L}_h^{\text{NTRU}}\),方便起见,后续将其记作\(\mathcal{L}_h\),显然向量\((\pmb{f},\pmb{g})\in\mathcal{L}_h\),接下来分析通过对\(\mathcal{L}_h\)进行格基规约得到向量\((\pmb{f},\pmb{g})\)的可能性: 因为\(\det(\mathcal{L}_h)=q^N\),所以有: \[
\left(\frac{2}{\sqrt{4\delta-1}}\right)^{2N-1}\sqrt{2N}\cdot|\det(\mathcal{L}_h)|^{1/2N}=\left(\frac{2}{\sqrt{4\delta-1}}\right)^{2N-1}\sqrt{2Nq}
\] 取\(\delta=\frac{3}{4}\),有: \[
\left(\frac{2}{\sqrt{4\delta-1}}\right)^{2N-1}\sqrt{2Nq}=(\sqrt{2})^{2N-1}\cdot\sqrt{2Nq}=2^N\sqrt{Nq}
\] 而因为\(f(x),g(x)\)都是三元多项式,所以: \[
||(\pmb{f},\pmb{g})||=\sqrt{4d+1}\le2^N\sqrt{Nq}=\left(\frac{2}{\sqrt{4\delta-1}}\right)^{2N-1}\sqrt{2N}\cdot|\det(\mathcal{L}_h)|^{1/2N}
\] 很显然,\((\pmb{f},\pmb{g})\)可以通过BKZ算法对格\(\mathcal{L}_h\)进行格基规约得到(LLL有时候不行),通过如下代码就可以构造出格并进行规约: L = matrix(ZZ, 2*N, 2*N)
h_coeff = [ZZ(x) for x in list(h)] # 有时候可能h要乘上一个pow(q, -1, p)
for i in range(N):
L[i, i] = 1
L[N + i, N + i] = q
for j in range(N):
L[i, N + j] = h_coeff[(j - i) % N]
res = L.BKZ()L = matrix(ZZ, 2*N, 2*N)
h_coeff = [ZZ(x) for x in list(h)]
for i in range(N):
L[i, i] = 1
L[N + i, N + i] = q
for j in range(N):
L[i, N + j] = h_coeff[(j - i) % N]
res = L.BKZ()[1]
ff = R([ZZ(x) for x in res[:N]])
print(ff)
fp = inv(Rp, ff)
a = center_lift(Rq, R, Rq(list(ff * e)))
b = center_lift(Rp, R, Rp(list(fp * a)))
print(b)
例题:[SCTF 2020]Lattice
题目地址:SCTF 2020:Lattice from base64 import b16encode
Zx.<x> = ZZ[]
n = 109
q = 2048
p = 3
Df = 9
Dg = 10
Dr = 11
def mul(f,g):
return (f * g) % (x^n-1)
def bal_mod(f,q):
g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
return Zx(g)
def random_poly(d):
assert d <= n
result = n*[0]
for j in range(d):
while True:
r = randrange(n)
if not result[r]: break
result[r] = 1-2*randrange(2)
return Zx(result)
def inv_mod_prime(f,p):
T = Zx.change_ring(Integers(p)).quotient(x^n-1)
return Zx(lift(1 / T(f)))
def inv_mod_powerof2(f,q):
assert q.is_power_of(2)
g = inv_mod_prime(f,2)
while True:
r = bal_mod(mul(g,f),q)
if r == 1: return g
g = bal_mod(mul(g,2 - r),q)
def keygen():
f = random_poly(Df)
while True:
try:
fp = inv_mod_prime(f,p)
fq = inv_mod_powerof2(f,q)
break
except:
f = random_poly(Df)
g = random_poly(Dg)
h = bal_mod(p * mul(fq,g),q)
pub_key = h
pri_key = [f,fp]
return pub_key,pri_key
def encrypt(m,h):
r = random_poly(Dr)
e = bal_mod(mul(h,r) + m,q)
return e
if __name__ == '__main__':
pub_key,pri_key = keygen()
flag=b'SCTF{***********}'[5:-1]
m = Zx(list(bin(int(b16encode(flag), 16))[2:]))
print(m)
e = encrypt(m,pub_key)
print('pub_key=')
print(pub_key)
print('e=')
print(e)from Crypto.Util.number import *
N = 109
q = 2048
p = 3
_R = PolynomialRing(ZZ, 'x')
R = _R.quotient(x^N - 1, 'x')
_Rp = PolynomialRing(Zmod(p), 'x')
Rp = _Rp.quotient(x^N - 1, 'x')
_Rq = PolynomialRing(Zmod(q), 'x')
Rq = _Rq.quotient(x^N - 1, 'x')
def center_lift(Rm, R, f):
modulo = ZZ(Rm(list(f)).base_ring()(-1)) + 1
l = [ZZ(x) if x <= modulo // 2 else ZZ(x) - modulo for x in list(f)]
return R(l)
def inv(Rm, f):
return Rm(f).inverse()
h = R("...")
e = R("...")
L = matrix(ZZ, 2*N, 2*N)
h_coeff = [ZZ(x) for x in list(h)]
for i in range(N):
L[i, i] = 1
L[N + i, N + i] = q
for j in range(N):
L[i, N + j] = h_coeff[(j - i) % N]
res = L.BKZ(blocksize=24)
for v in res:
fc = list(v[:N])
c0, c1, c_1 = fc.count(0), fc.count(1), fc.count(-1)
if c0 == 100 and c1 + c_1 == 9:
f = R(fc)
Fp = inv(Rp, f)
a = center_lift(Rq, R, Rq(list(f * e)))
b = center_lift(Rp, R, Rp(list(Fp * a)))
s = "".join([str(x) for x in ct])
pad = 8 - len(s) % 8
for i in range(pad + 1):
print(long_to_bytes(int('0' * i + s + '0' * (pad - i), 2)))
breakSCTF{@#26f35b89d3#@}
