格密码
参考资料：
格（Lattice）
格的概念
定义：一个\(n\)维的格\(\mathcal{L}\)是\(\mathbb{R}^{n}\)的一个离散可加的子群. 对于格\(\mathcal{L}\)，其可以被表示为由\(\mathbb{R}^{n}\)上\(m\)个线性无关的基向量\(\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_m\}\)组成的基\(\pmb{B}\)，向量的个数\(m\)被称为格\(\mathcal{L}\)的秩，所以格\(\mathcal{L}\)也能表示为： \[ \mathcal{L}=\mathcal{L}(\pmb{B})=\left\{\sum_{i=1}^{m}a_i\pmb{b}_i|a_i\in\mathbb{Z},i=1,2,\cdots,m\right\} \] 格的很多性质与记号与线性空间（向量空间）类似。 逐次最小长度：对于一个秩维\(n\)的格\(\mathcal{L}\)，对于\(i\in\{1,2,\cdots n\}\)，若\(r\)是使得格\(\mathcal{L}\)拥有\(i\)个长度最大为\(r\)且线性无关的向量的最小值，则称\(r\)为格\(\mathcal{L}\)的第\(i\)逐次最小长度，记为\(\lambda_i(\mathcal{L})=r\) 关于逐次最小长度，我们有闵可夫斯基（Minkowski）第一定理： 闵可夫斯基（Minkowski）第一定理：设\(\mathcal{L}\)是一个\(n\)维满秩格，则： \[ \lambda_1(\mathcal{L})\le\sqrt{n}|\det(\mathcal{L})|^{1/n} \] 闵可夫斯基第一定理表明我们可以以\(\lambda_1(\mathcal{L})\)为标准来评判格中向量的长度.
关于格的问题
最短向量问题（Shortest Vector Problem, \(\text{SVP}\)）：给定格\(\mathcal{L}\)的基\(\pmb{B}\)，找到格\(\mathcal{L}\)上的一个非零向量\(\pmb{v}\)满足\(||\pmb{v}||=\lambda_1(\mathcal{L})\). 最近向量问题（Closest Vector Problem, \(\text{CVP}\)）：给定格\(\mathcal{L}\)的基\(\pmb{B}\)以及一个目标向量\(\pmb{t}\)（不一定在格\(\mathcal{L}\)上），找到格\(\mathcal{L}\)上的一个非零向量\(\pmb{v}\)满足 \[ ||\pmb{v}-\pmb{t}||=\min_{\pmb{w}\in\mathcal{L}}||\pmb{w}-\pmb{t}|| \] 上述问题均为NP-Hard问题，这些问题的宽松版本如下： 近似最短向量问题（Approximate Shortest Vector Problem, \(\text{SVP}_{\gamma}\)）：给定格\(\mathcal{L}\)的基\(\pmb{B}\)与近似因子\(\gamma\)，找到格\(\mathcal{L}\)上的一个非零向量\(\pmb{v}\)满足\(||\pmb{v}||\le\gamma\cdot\lambda_1(\mathcal{L})\). 近似最近向量问题（Approximate Closest Vector Problem, \(\text{CVP}_{\gamma}\)）：给定格\(\mathcal{L}\)的基\(\pmb{B}\)、一个目标向量\(\pmb{t}\)（不一定在格\(\mathcal{L}\)上）以及一个近似因子\(\gamma\)，找到格\(\mathcal{L}\)上的一个非零向量\(\pmb{v}\)满足 \[ ||\pmb{v}-\pmb{t}||=\gamma\cdot\min_{\pmb{w}\in\mathcal{L}}||\pmb{w}-\pmb{t}|| \] 而\(\text{SVP}_{\gamma}\)与\(\text{CVP}_{\gamma}\)对于确定的参数均存在有效的解决方案，所以我们可以通过解决\(\text{SVP}_{\gamma}\)与\(\text{CVP}_{\gamma}\)来近似地解决\(\text{SVP}\)与\(\text{CVP}\). 我们可以通过格基规约来解决上述两个可计算问题.
格基规约
格基规约的目标是将一个任意一个格转化为另外一个基相同但是具有更短、更多的正交向量。由于我们要找的是“短向量”，所以格基规约可能会提供解决近似最短向量问题的方法.
LLL算法
LLL算法是一个迭代算法，由Lenstra、Lenstra与Lovász提出. 这个迭代算法的第一步是通过施密特正交化获得基\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)的一组正交基，通过施密特正交化，我们可以将格基进行约减，对于上面的基\(\pmb{B}\)，施密特正交化过程如下： \[ \begin{cases} \pmb{b}_i^{*}=\pmb{b}_i,&i=1\\ \pmb{b}_i^{*}=\pmb{b}_i-\sum_{j=1}^{i-1}\mu_{i,j}\pmb{b}_j^{*},&1<i\le n \end{cases}\kern{25pt}\mu_{i,j}=\frac{\langle\pmb{b}_i,\pmb{b}_{j}^{*}\rangle}{\langle\pmb{b}^{*}_{j},\pmb{b}^{*}_{j}\rangle} \] 而对于\(\delta\in(\frac{1}{4},1)\)，如果基\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)满足：
- （尺寸约减，size-reduction）对于任意\(i>j\)，有\(|\mu_{i,j}|\le\frac{1}{2}\)；
- （Lovász条件，Lovász condition）对于任意\(i\in\{1,2,\cdots,n-1\}\)，有\((\delta-\mu_{i+1,i}^{2})||\pmb{b}_{i}^{*}||^{2}\le||\pmb{b}_{i+1}^{*}||^2\)
则称基\(\pmb{B}\)为\(\delta\)-LLL约减基，通过结合这两个条件，Lenstra、Lenstra与Lovász给出了LLL算法： 
而对于格中最短向量的下界，我们有如下定理： 设格基\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)对应的施密特正交基为基\(\pmb{B}^*=\{\pmb{b}_1^*,\pmb{b}_2^*,\cdots,\pmb{b}_n^*\}\)，则有： \[
\lambda_1(\mathcal{L}(\pmb{B}))\ge\min_{i\in\{1,\cdots,n\}}||\pmb{b}^{*}_{i}||
\] 通过这个定理，我们可以导出如下命题： 假若\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)是一个\(\delta\)-LLL约减基，则必然有： \[
||\pmb{b}_1||\le\left(\frac{2}{\sqrt{4\delta-1}}\right)^{n-1}\sqrt{n}\cdot|\det(\mathcal{L})|^{1/n}
\]
这条式子往往可以帮助我们判断一个格基是否能通过LLL来约减出最短向量. 在sage中内置了现成的LLL算法，例如我们要解决A Gentle Tutorial for Lattice-Based Cryptanalysis中的例3.12（如下图）：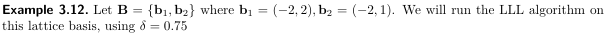 
则可以通过下面的步骤来获得结果： 
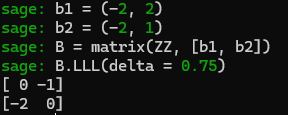显然可以得到结果为\(\pmb{b}_1^*=(0,-1),\pmb{b}_2^*=(-2,0)\).
解决CVP
LLL算法同样可以用来解决近似最近向量问题，但是需要结合Babai最近平面算法或者Kannan嵌入法
Babai最近平面算法（Babai’s Nearest Plane Algorithm）
Babai最近平面算法首先要获得输入格的约减基\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)，然后对于目标向量\(\pmb{t}\)，我们令\(\pmb{t}'=\pmb{t}-c_n\pmb{b}_n\)，其中：\(c_n=\lceil\langle\pmb{t},\pmb{b}^*_{n}\rangle/\langle\pmb{b}^*_{n},\pmb{b}^*_{n}\rangle\rfloor\)（其中\(\lceil\cdot\rfloor\)表示四舍五入），然后对前\(n-1\)个向量与\(\pmb{t}'\)进行操作，得到\(\pmb{t}''=\pmb{t}'-c_{n-1}\pmb{b}_{n-1}\)，其中\(c_n=\lceil\langle\pmb{t}',\pmb{b}^*_{n-1}\rangle/\langle\pmb{b}^*_{n-1},\pmb{b}^*_{n-1}\rangle\rfloor\)，以此类推，就可以得到完整的Babai最近平面算法： 
Kannan嵌入法
Kannan嵌入法是通过将目标向量嵌入格基，从而将CVP转化为SVP进行求解，设输入的格基为\(\pmb{B}=\{\pmb{b}_1,\pmb{b}_2,\cdots,\pmb{b}_n\}\)，而目标向量为\(\pmb{t}=(t_1,t_2,\cdots,t_n)\)，我们设CVP的解为\(c_1\pmb{b}_1+c_2\pmb{b}_2+\cdots+c_n\pmb{b}_n\)，即： \[ \pmb{t}\approx\sum_{i=1}^{n}c_i\pmb{b}_i \] 也就有： \[ \pmb{t}=\sum_{i=1}^{n}c_i\pmb{b}_i+\pmb{e} \] 其中\(||\pmb{e}||\)很小，所以我们就可以构造出一个\(n+1\)维的格： \[ \pmb{B}'= \left(\begin{matrix} \pmb{B}&0\\ \pmb{t}&q \end{matrix}\right) \] 因为有： \[ (-c_1,-c_2,\cdots,-c_n,1)\pmb{B}'=(\pmb{e},q) \] 所以这个格显然包含短向量\((\pmb{e},q)\)，由此我们就可以得到CVP的解为\(\pmb{t}-\pmb{e}\). 在这里，整数\(q\)称为嵌入因子，它会影响到通过LLL算法寻找正确向量的成功率，应根据实际情况选取.
格在密码学中的应用
背包问题（Knapsack Problem）
背包问题是NP完全问题，其经常被用于作为公钥密码体系的陷阱门。在密码学中，背包问题的常见版本为子集和问题，即：给定\(n\)个正数\(a_1,a_2,\cdots,a_n\)与一个整数\(s\)，寻找集合\(\{a_1,a_2,\cdots,a_n\}\)的子集使得其和为\(s\)。也就是找到\(e_1,e_2,\cdots,e_n\in\{0,1\}\)使得： \[ s=\sum_{i=1}^{n}e_ia_i \]
低密度子集和问题
集合\(\{a_1,a_2,\cdots,a_n\}\)的密度\(d\)可以通过下式计算： \[
d=\frac{n}{\log_2{\max_{i\in\{1,2,\cdots,n\}}(a_i)}}
\] 研究表明，当\(d<0.9408\)时，我们可以将子集和问题转换为求解SVP. 一般策略为构造一个格，其中有一个短向量包含\(\{e_1,e_2,\cdots,e_n\}\)，这样我们就可以构造出下面的格基矩阵： \[
\pmb{B}=\left(\begin{matrix}
1&&&&a_1\\
&1&&&a_2\\
&&\ddots&&\vdots\\
&&&1&a_n\\
&&&&s
\end{matrix}\right)
\] 显然线性组合\((e_1,e_2,\cdots,e_n,-1)\)会生成一个短向量\((e_1,e_2,\cdots,e_n,-1)\pmb{B}=(e_1,e_2,\cdots,e_n,0)\)，所以我们的预期是通过LLL算法对上述格进行规约得到这个短向量，但是这个方法在密度比较高的时候会失效，所以Coster等人提出了CJLOSS算法，使得我们可以在\(d<0.9408\)的时候通过将子集和问题转换为SVP从而在多项式时间内求解这个问题，CJLOSS算法中构造的格为： \[
\pmb{B}'=\left(\begin{matrix}
1&&&&Na_1\\
&1&&&Na_2\\
&&\ddots&&\vdots\\
&&&1&Na_n\\
\frac{1}{2}&\frac{1}{2}&\cdots&\frac{1}{2}&Ns
\end{matrix}\right)
\] 其中整数\(N>\sqrt{n}\)，在这个格内，线性组合\((e_1,e_2,\cdots,e_n,-1)\)会生成另外一个短向量： \[
(e_1,e_2,\cdots,e_n,-1)\pmb{B}'=(e_1-\frac{1}{2},e_2-\frac{1}{2},\cdots,e_n-\frac{1}{2},0)
\] 显然这条短向量的模为\(\frac{\sqrt{n}}{2}\)，我们很容易可以通过LLL算法求解出这条短向量（这个短向量一般是规约后的格的第一个向量，且前\(n\)个元素往往为\(\frac{1}{2}-e_i\)）。 使用sage通过CJLOSS算法求解低密度子集和的代码如下： def CJLOSS(A, s):
n = len(A)
N = ceil(sqrt(n))
L = matrix(QQ, n + 1)
for i in range(n):
L[i, i] = 1
L[n, i] = 1/2
L[i, n] = N * A[i]
L[n, n] = N * s
res = L.LLL()
for v in res:
if all(x in [-1/2, 1/2] for x in v[:-1]):
out = [1/2 - a for a in v[:-1]]
return out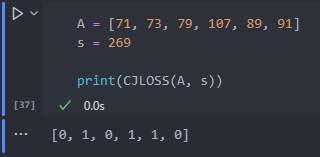
所以可以得到和为\(269\)的一个子集为\(\{73,107,89\}\).
低密度多重子集和问题
通过对子集和问题的扩展，我们可以得到多重子集和问题：给定\(kn\)个正整数\(a_{1,1},a_{1,2}\cdots,a_{k,n}\)以及\(k\)个整数\(s_1,\cdots,s_k\)，找到\(e_1,e_2,\cdots,e_n\in\{0,1\}\)满足对任意\(j\in{1,2,\cdots,k}\)： \[ s_j=\sum_{i=1}^{n}e_ia_{j,i} \] 实际上多重子集和问题总体与普通子集和问题差不多，但是集合更多，此时我们通过下式对密度\(d\)进行计算： \[ d=\frac{n}{k\log_2{\max_{\begin{matrix}\end{matrix}}(a_{j,i})}} \] 根据潘彦斌等人研究可以得出，当\(d<0.9408\)时，我们可以通过构造如下格来将低密度多重子集和问题转换为SVP进行求解： \[ \pmb{B}=\left(\begin{matrix} 1&&&&0&Na_{1,1}&Na_{2,1}&\cdots&Na_{k,1}\\ &1&&&0&Na_{1,2}&Na_{2,2}&\cdots&Na_{k,2}\\ &&\ddots&&\vdots&\vdots&\vdots&\ddots&\vdots\\ &&&1&0&Na_{1,n}&Na_{2,n}&\cdots&Na_{k,n}\\ \frac{1}{2}&\frac{1}{2}&\cdots&\frac{1}{2}&\frac{1}{2}&Ns_1&Ns_2&\cdots&Ns_k \end{matrix}\right) \] 其中整数\(N>\sqrt{\frac{n+1}{4}}\)，此时在这个格内，线性组合\((e_1,e_2,\cdots,e_n,-1)\)会生成一个短向量： \[ (e_1,e_2,\cdots,e_n,-1)\pmb{B}=(e_1-\frac{1}{2},e_2-\frac{1}{2},\cdots,e_n-\frac{1}{2},-\frac{1}{2},0,\cdots,0) \] 通过LLL算法我们就可以得到这个短向量.
低密度模子集和问题与低密度多重模子集和问题
通过对子集和问题的扩充，我们可以得到模子集和问题：给定\(n\)个模\(M\)下的正整数\(a_1,a_2,\cdots,a_n\)，再给出一个整数\(s\)，找到\(e_1,e_2,\cdots,e_n\in\{0,1\}\)，使得： \[ s\equiv\sum_{i=1}^{n}e_ia_i\pmod{M} \] 从而可以推广为多重模子集和问题：给定\(kn\)个模\(M\)下的正整数\(a_{1,1},a_{1,2}\cdots,a_{k,n}\)以及\(k\)个整数\(s_1,\cdots,s_k\)，找到\(e_1,e_2,\cdots,e_n\in\{0,1\}\)满足对任意\(j\in{1,2,\cdots,k}\)： \[ s_j\equiv\sum_{i=1}^{n}e_ia_{j,i}\pmod{M} \] 实际上，模子集和问题问题可以视作\(k=1\)的多重模子集和问题，我们可以通过下式对多重模子集和问题的密度\(d\)进行计算： \[ d=\frac{n}{k\log_2M} \] 根据潘彦斌等人研究可以得出，当\(d<0.9408\)且\(k=\omicron\left(\frac{n}{\log_2((n+1)\sqrt{n}+1)}\right)\)时，我们可以通过构造如下格来将低密度多重模子集和问题转换为SVP进行求解： \[ \pmb{B}=\left(\begin{matrix} 1&&&&0&Na_{1,1}&Na_{2,1}&\cdots&Na_{k,1}\\ &1&&&0&Na_{1,2}&Na_{2,2}&\cdots&Na_{k,2}\\ &&\ddots&&\vdots&\vdots&\vdots&\ddots&\vdots\\ &&&1&0&Na_{1,n}&Na_{2,n}&\cdots&Na_{k,n}\\ &&&&&NM&&&\\ &&&&&&NM&&\\ &&&&&&&\ddots&\\ &&&&&&&&NM\\ \frac{1}{2}&\frac{1}{2}&\cdots&\frac{1}{2}&\frac{1}{2}&Ns_1&Ns_2&\cdots&Ns_k \end{matrix}\right) \] 使用LLL算法进行规约就可以得到目标短向量\((e_1-\frac{1}{2},e_2-\frac{1}{2},\cdots,e_n-\frac{1}{2},-\frac{1}{2},0,\cdots,0)\).
隐藏数问题（Hidden Number Problem，HNP）
隐藏数问题的形式一般为给定一个质数\(p\)，令\(\alpha\in[1,p-1]\)作为“被隐藏的数字”，给定\(m\)个数对\(\{(t_i,a_i)\}^{m}_{i=1}\)使得： \[ \beta_i-t_i\alpha+a_i\equiv0\pmod{p} \] 其中\(|\beta_i|<K<p\)，我们需要从中恢复出\(\alpha\). 为解决这类问题，我们可以重写\(\beta_i-t_i\alpha+a_i\equiv0\pmod{p}\)为\(\beta_i+a_i=t_i\alpha+k_ip\)，这样我们就可以构造出下面的格： \[ \pmb{B}=\left(\begin{matrix} p&&&&\\ &p&&&\\ &&\ddots&&\\ &&&p&\\ t_1&t_2&\cdots&t_m&\frac{1}{p} \end{matrix}\right) \] 对于向量\(\pmb{v}=(k_1,\cdots,k_m,\alpha)\)有\(\pmb{v}\pmb{B}=(\beta_1+a_1,\cdots,\beta_m+a_m,\alpha/p)\)，显然这个向量并不是很短，但是我们注意到： \[ \pmb{v}\pmb{B}=(a_1,\cdots,a_m,0)+(\beta_1,\cdots,\beta_m,\alpha/p) \] 那么令\(\pmb{t}=(a_1,\cdots,a_m,0),\pmb{u}=(\beta_1,\cdots,\beta_m,\alpha/p)\)，我们就可以得到： \[ \pmb{v}\pmb{B}-\pmb{t}=\pmb{u} \] 其中\(||\pmb{u}||<\sqrt{m+1}K\)，显然我们可以通过将求解HNP转换为求解CVP，通过Kannan嵌入法，令嵌入因子为\(K\)，我们就可以得到下面的格： \[ \pmb{B}'=\left(\begin{matrix} p&&&&&\\ &p&&&&\\ &&\ddots&&&\\ &&&p&&\\ t_1&t_2&\cdots&t_m&\frac{K}{p}&\\ a_1&a_2&\cdots&a_m&&K \end{matrix}\right) \] 其包含向量\(\pmb{u}'=(\beta_1,\cdots,\beta_m,K\alpha/p,-K)\)，且\(||\pmb{u}'||<\sqrt{m+2}K\)，\(\det(\pmb{B}')=p^{m-1}K^2\)，显然有： \[ ||\pmb{u}'||<\sqrt{m+2}K<\left(\frac{2}{\sqrt{4\delta-1}}\right)^{m+1}\sqrt{m+2}|\det(\pmb{B}')|^{1/(m+2)} \] 所以我们可以通过LLL来找到短向量\(\pmb{u}'\)，但是这个向量并不是最短的，因为格上存在另一个向量\((0,\cdots,0,K,0)\)，它比\(\pmb{u}'\)更短，所以\(\pmb{u}'\)一般在规约后的第二个向量.
扩展隐藏数问题（Extended Hidden Number Problem，EHNP）
通过对一般的隐藏数问题的扩展我们可以得到扩展隐藏数问题：给定素数\(p\)，对整数\(x\in[1,p-1]\)，有： \[ x=\overline{x}+\sum_{j=1}^{m}2^{\pi_{j}}x_j \] 其中\(\overline{x}\)以及\(\pi_j\)均已知，而未知整数\(x_j\)对于一个已知的整数\(\nu_j\)满足\(0\le x_{j}<2^{\nu_j}\)，给出\(d\)条方程： \[ \alpha_i\sum_{j=1}^{m}2^{\pi_j}x_j+\sum_{j=1}^{l_i}{\rho_{i,j}k_{i,j}}\equiv\beta_{i}-\alpha_i\overline{x}\pmod{p} \] 其中对于\(1\le i\le d\)，\(\alpha_i\not\equiv 0\pmod{p}\)，\(\rho_{i,j}\)以及\(\beta_i\)均为已知的整数，未知正整数\(k_{i,j}\)的上界为\(2^{\mu_{i,j}}\)且\(\mu_{i,j}\)已知，则扩展隐藏数问题（EHNP）则是通过上述条件恢复\(x\). 为解决EHNP，我们可以构造格： \[ \pmb{B}=\left(\begin{matrix} p\pmb{I}_d&&\\ \pmb{A}&\pmb{X}&\\ \pmb{R}&&\pmb{K} \end{matrix}\right) \] 其中： \[ \begin{aligned} &\pmb{A}=\left(\begin{matrix} \alpha_{1}2^{\pi_1}&\alpha_{2}2^{\pi_1}&\cdots&\alpha_{d}2^{\pi_1}\\ \alpha_{1}2^{\pi_2}&\alpha_{2}2^{\pi_2}&\cdots&\alpha_{d}2^{\pi_2}\\ \vdots&\vdots&\ddots&\vdots\\ \alpha_{1}2^{\pi_m}&\alpha_{2}2^{\pi_m}&\cdots&\alpha_{d}2^{\pi_m}\\ \end{matrix}\right)\\ &\pmb{X}=diag\left(\frac{\delta}{2^{\nu_{1}}},\frac{\delta}{2^{\nu_{2}}},\cdots,\frac{\delta}{2^{\nu_{m}}}\right)\\ &\pmb{R}=\left(\begin{matrix} \rho_{1,1}&&\\ \rho_{1,2}&&\\ \vdots\\ \rho_{1,l_1}&&\\ &\ddots&\\ &&\rho_{d,1}\\ &&\rho_{d,2}\\ &&\vdots\\ &&\rho_{d,l_{d}} \end{matrix}\right)\\ &\pmb{K}=diag\left(\frac{\delta}{2^{\mu_{1,1}}},\cdots,\frac{\delta}{2^{\mu_{1,l_{1}}}},\cdots,\frac{\delta}{2^{\mu_{d,1}}},\cdots,\frac{\delta}{2^{\mu_{d,l_d}}}\right) \end{aligned} \] 设\(L=l_1+l_2+\cdots+l_d\)，\(D=d+m+L\)，计算： \[ \kappa_{D}=\frac{2^{D/4}(m+L)^{1/2}+1}{2} \] 通过\(\kappa_{D}\)，我们可以得到\(\delta\)满足\(0<\delta\kappa_{D}<1\)。令 \[ \pmb{v}=(\beta_{1}-\alpha_{i}\overline{x},\cdots,\beta_{d}-\alpha_{d}\overline{x},\frac{\delta}{2},\cdots,\frac{\delta}{2}) \] 我们需要根据上述的\(\delta\)构造格\(\mathcal{L}=\mathcal{L}(\pmb{B},\delta)\)，在格\(\mathcal{L}\)中找到向量\(\pmb{u}\)使得： \[ ||\pmb{u}-\pmb{v}||\le 2^{\frac{D}{4}}\min_{\pmb{t}\in\mathcal{L}}||\pmb{v}-\pmb{t}|| \] 通过LLL算法对我们构造的格进行规约可以得到： \[ \pmb{u}=\left(\beta_{1}-\alpha_{i}\overline{x},\cdots,\beta_{d}-\alpha_{d}\overline{x},\frac{x_1\delta}{2^{\nu_1}} ,\cdots,\frac{x_m\delta}{2^{\nu_m}},\frac{k_{1,1}\delta}{2^{\mu_{1,1}}},\cdots,\frac{k_{1,l_1}\delta}{2^{\mu_{1,l_{1}}}},\cdots,\frac{k_{d,1}\delta}{2^{\mu_{d,1}}},\cdots,\frac{k_{d,l_d}\delta}{2^{\mu_{d,l_d}}}\right) \] 然后令\(x_{j}'=\frac{1}{\delta}(\pmb{u}_{d+j}2^{\nu_{j}})\)（\(1\le j\le m\)），最后计算： \[ x'=\overline{x}+\sum_{j=1}^{m}2^{\pi_j}x'_{j}\mod{p} \] 这样得到的\(x'\)就是我们需要的\(x\). 在论文Extended Hidden Number Problem and Its Cryptanalytic Applications中还提及了一种通过狄利克雷近似计算双洞隐藏数问题（Hidden Number Problem with Two Holes， HNP-2H），具体方法与步骤在通过狄利克雷近似解决HNP-2H | Triode Field有写.
Coppersmith方法
Howgrave-Graham定理
设\(h(x_1,\cdots,x_n)\in\mathbb{Z}[x_1,\cdots,x_n]\)是一个由\(\omega\)个单项式组成的多项式，如果：
- 存在\(|r_1|<X_1,\cdots,|r_n|<X_n\)，有\(f(r_1,\cdots,r_n)\equiv0\pmod{N}\)
- \(||h(x_1X_1,\cdots,x_nX_n)||<\frac{N}{\sqrt{\omega}}\)
那么\(f(r_1,\cdots,r_n)=0\)在整数域同样成立.
这个定理是Coppersmith方法的关键所在。
一元Coppersmith
对于度为\(k\)的一元本原多项式\(p(x)=x^{k}+a_{k-1}x^{k-1}+\cdots+a_{1}x+a_{0}\in\mathbb{Z}[x]\)，Coppersmith方法可以找到方程\(p(x)\equiv0\pmod{N}\)（其中\(N\)是一个合数）的一个小根\(x\equiv x_0\pmod{N}\)（\(|x_{0}|<X\)，其中\(X\)是一个自然数，且\(X\le N^{1/k}\)） 这个算法的主要思想就是构造一个多项式\(h(x)\)使得\(h(x_0)=0\)，而求解\(h(x)=0\)这个方程是很简单的，所以我们可以将求解\(p(x)\equiv0\pmod{N}\)这一任务转化为求解\(h(x)=0\)。我们可以构造格： \[
\pmb{B}=\left(\begin{matrix}
N&&&&&\\
&XN&&&&\\
&&X^2N&&&\\
&&&\ddots&&\\
&&&&X^{k-1}N&\\
a_0&a_1X&a_2X^2&\cdots&a_{d-1}X^{d-1}&X^{d}
\end{matrix}\right)
\] 然后通过LLL规约得到一个矩阵： \[
\pmb{B}'=\left(\begin{matrix}
b_0&b_1&\cdots&b_{d-1}&b_{d}\\
*&*&\cdots&*&*\\
\vdots&\vdots&&\vdots&\vdots\\
*&*&\cdots&*&*
\end{matrix}\right)
\] 则有： \[
h(Xx)=b_dx^{d}+b_{d-1}x^{d-1}+\cdots+b_{1}x+b_0
\] 可以得到： \[
h(x)=\left(\frac{b_d}{X^d}\right)x^{d}+\left(\frac{b_{d-1}}{X^{d-1}}\right)x^{d-1}+\cdots+\left(\frac{b_1}{X}\right)x+b_0
\] 解该方程得到的整数解就有可能是我们要的\(x_0\)。 在实际应用中，我们可以直接利用sage的small_roots来进行求解。
多元Coppersmith
那堆东西暂时没看懂，先贴个从某些地方搜刮来的板子
def small_roots(f, bounds, m=1, d=None): |
一般维纳攻击的格方法
维纳方法：对于\(N=pq\)，假设\(\lambda({N})\)与\(e\)均与\(N\)接近，而且解密指数\(d<N^{1/4}\)，那么因为\(e\)与\(d\)满足\(ed-k\lambda(N)=1\)，所以令\(\lambda(N)=(p-1)(q-1)/g\)，又令\(s=1-p-q\)，就可以得到： \[ edg-kN=g+ks \] 那么有： \[ \frac{e}{N}-\frac{k}{dg}=\frac{ks}{dgN}+\frac{1}{dN} \] 由于\(e\approx N\)，\(|s|\approx N^{1/2}\)，那么可以得到\(\frac{k}{dg}\approx1\)，所以上述方程的值约等于\(N^{-1/2}\)，由勒让德定理，如果\(N^{-1/2}<1/[2(dg)^2]\)，那么\(\frac{k}{dg}\)会是\(e/N\)的渐进分数，所以我们可以通过连分数来得到\(d\)，或者分解出\(p,q\)，上述讨论中一般情况下\(g=1\)。 令\(g=1\)，实际上此时\(\lambda(N)=\varphi(N)\)，我们注意到，在上述条件下得到的\(ed-kN=1+ks\)一式存在线性关系，所以可以考虑使用格来求解，考虑构造如下格： \[ \pmb{B}=\left(\begin{matrix} 1&e\\ 0&-N \end{matrix}\right) \] 其中目标向量为\(\pmb{v}=(d,1+ks)\)，其中\(s=1-p-q\)，可以知道\(|s|\approx N^{1/2}\)，\(d<N^{1/4}\)，则有\(|\det(\pmb{B})|=N\)，可以知道 \[ ||\pmb{v}||=\sqrt{d^2+(1+ks)^2}>\sqrt{2}N^{1/2}>\sqrt{2}|\det(\pmb{B})|^{1/2} \] 显然，通过闵可夫斯基第一定理，我们几乎不可能通过规约得到我们的目标向量，那么我们要进行格基配平，根据分析，我们构造如下格： \[ \pmb{B}'=\left(\begin{matrix} 2^{\alpha}&e\\ 0&-N \end{matrix}\right) \] （其中\(\alpha\)是\(N\)的比特数的\(1/2\)），这样就可以通过LLL算法规约得到目标向量\((2^{\alpha}d,1+ks)\).