同源(1)——SIDH
参考资料:
前置知识
超奇异(supersingular)椭圆曲线
对于\(GF(p^r)\)下的椭圆曲线\(E\),若\(|E|\equiv 1\pmod{p}\),则称该曲线为超奇异椭圆曲线
\(j\)-不变量(\(j\)-invariant)
对于一条由方程\(y^2=x^3+ax+b\)定义的椭圆曲线\(E\),其\(j\)-不变量的定义为: \[
j(E)=
1728\cdot\frac{4a^3}{4a^3+27b^2}
\] 当且仅当两条定义在代数闭包\(\overline{k}\)上的曲线\(E\)与\(E'\)的\(j\)-不变量相同时这两条曲线同构,即存在点到点之间的双射\(\phi\)使得: \[
\phi:E\mapsto E'
\] 通过参考资料2我们可以知道对于SIDH,其主要作用于有限域\(GF(p)\)的二次扩展(即\(GF(p^2)\),其中\(p\equiv 3\pmod{4}\)),方便起见,我们通常将这个二次扩展域中的元素表示为\(u+vi\)(其中\(u,v\in GF(p)\),\(i^2\equiv-1\pmod{p}\)),定义在这个二次扩展域上的超奇异\(j\)-不变量的个数为\(\lfloor p/12\rfloor+z\),这些超奇异\(j\)-不变量每一个都对应一条同构意义下的超奇异曲线,其中\(z\in\{0,1,2\}\),\(z\)的取值取决于\(p\mod 12\),具体如下(参考资料3,P264): \[
z=\begin{cases}
0&,p\equiv1\pmod{12}\\
1&,p\equiv5\pmod{12}\\
1&,p\equiv7\pmod{12}\\
2&,p\equiv11\pmod{12}\\
\end{cases}
\] 例如对于参考资料2中的例子(即\(p=431\)),\(GF(p^2)\)中的\(\lfloor p/12\rfloor+2=37\)个\(j\)-不变量分别对应一条同构意义下的超奇异曲线,这些\(j-\)不变量如下图所示: 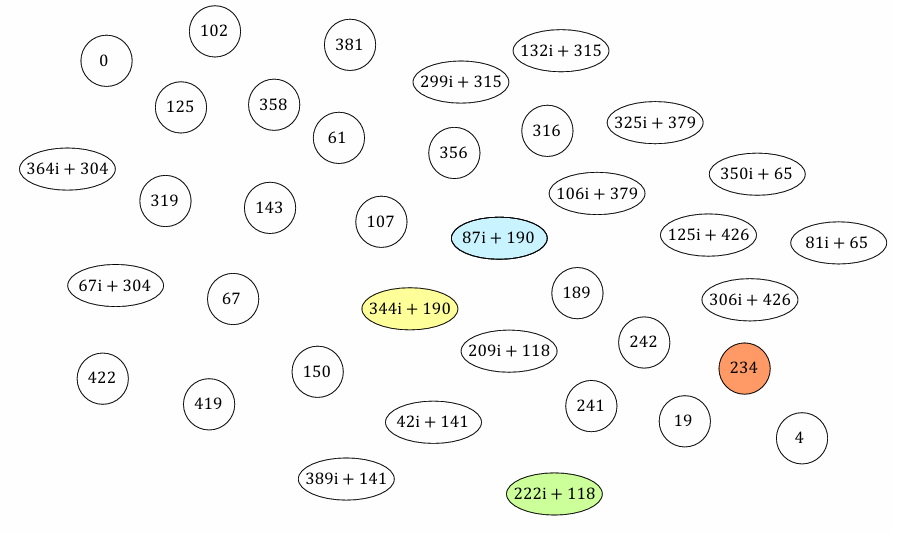 关于\(j\)-不变量与曲线间同构的关系,参考资料2给出了一个例子:对于\(GF(431^2)\)下的两条曲线: \[
\begin{aligned}
E_1:y^2=x^3+(208i+161)x^2+x\\
E_2:y^2=x^3+(172i+162)x^2+x\\
\end{aligned}
\] 可以计算出\(j(E_1)=j(E_2)=364i+304\),那么我们可以通过如下代码来求出\(E_1\)到\(E_2\)的同构映射:
关于\(j\)-不变量与曲线间同构的关系,参考资料2给出了一个例子:对于\(GF(431^2)\)下的两条曲线: \[
\begin{aligned}
E_1:y^2=x^3+(208i+161)x^2+x\\
E_2:y^2=x^3+(172i+162)x^2+x\\
\end{aligned}
\] 可以计算出\(j(E_1)=j(E_2)=364i+304\),那么我们可以通过如下代码来求出\(E_1\)到\(E_2\)的同构映射: p = 431
R.<i> = GF(p^2, modulus=[1, 0, 1])
E1 = EllipticCurve(R, [0, 208*i+161, 0, 1, 0])
E2 = EllipticCurve(R, [0, 172*i+162, 0, 1, 0])
print(E1.j_invariant())
print(E2.j_invariant())
phi = E1.isomorphism_to(E2)
print(phi.rational_maps())
蒙哥马利(Montgomery)曲线
在椭圆曲线密码学中常用的椭圆曲线为形如\(y^2=x^3+ax+b\)方程所确定的曲线,这类方程一般称为魏尔斯特拉斯(Weierstrass)方程,这类方程确定的曲线一般称为魏尔斯特拉斯形式的椭圆曲线,还有另外一种形式的椭圆曲线是由方程\(y^2=x^3+Ax^2+x\)所定义的,这类椭圆曲线被称为蒙哥马利曲线,对于一条蒙哥马利曲线\(E:y^2=x^3+Ax^2+x\),其\(j\)-不变量为: \[
j(E)=\frac{256(A^2-3)^3}{A^2-4}
\] 任意一条椭圆曲线都可以转换为\(j\)-不变量相同(亦即同构)的蒙哥马利曲线,在sage中,我们可以通过montgomery_model来将一条椭圆曲线转换为蒙哥马利曲线,例如我们要将魏尔斯特拉斯形式的椭圆曲线: \[
E:y^2=x^3+312589632x+654443578\pmod{1912812599}
\] 转换为对应的蒙哥马利曲线,则可以通过如下代码进行: p = 1912812599
a = 312589632
b = 654443578
E = EllipticCurve(GF(p), [a, b])
E_M = print(E.montgomery_model()
同源
同源实际上就是一条曲线到另一条曲线或者一条曲线到自身的映射,其本质为同态,可以简单地表达为\((x,y)\mapsto(f(x,y),g(x,y))\),其中\(f,g\)是两个函数。在之后的讨论中将主要以蒙哥马利曲线为主,因为蒙哥马利曲线之间的映射可以单纯通过对\(x\)进行映射\(x\mapsto f(x)\)来表示出曲线间完整的映射,其完整映射形式为: \[
(x,y)\mapsto(f(x),cyf'(x))
\] 其中\(c\)是固定常数,\(f'\)为\(f\)的导函数. 对于一条蒙哥马利曲线\(E:y^2=x^3+ax^2+x\),可以得到一个\(E\)到\(E\)的同构映射: \[
[2]:E\mapsto E, x\mapsto\frac{(x^2-1)^2}{4x(x^2+ax+1)}
\] 这个映射一般称为二倍点映射,事实上,我们令分母\(4x(x^2+ax+1)=0\),可以得到三个根\(0,\alpha,\frac{1}{\alpha}\)(其中\(\alpha\)满足\(\alpha^2+a\alpha+1\)),我们就可以得到曲线上阶为\(2\)的点:\((0,0),(\alpha,0),(\frac{1}{\alpha},0)\),这三个点的集合就是映射\([2]\)的核,记为\(\ker([2])\),它是椭圆曲线群\(E\)的一个子群,同构于\(\mathbb{Z}_2\times\mathbb{Z}_2\),这上面的点称为\(2\)-torsion,事实上对于任意一条椭圆曲线都有其对应的\(\ker([2])\) 例如对于\(GF(431^2)\)下的椭圆曲线\(E:y^2=x^3+x\),可以通过如下代码得到对应的上述映射: R.<i> = GF(p^2, modulus=[1, 0, 1])
a = 1
E = EllipticCurve(R, [1, 0])
print(E._multiple_x_numerator(2))
print(E._multiple_x_denominator(2))division_points方法对\(E\)的零元开二次根来达到这一目的:E(0).division_points(2),参考资料2中给出了这样一个图来描述\(\ker([2])\):  在这里每个“花瓣”对应一个二阶循环子群。相应的,还有三倍点映射\([3]\),对于蒙哥马利曲线\(E:y^2=x^3+ax^2+x\),其对应三倍点映射为: \[
[3]:E\mapsto E:x\mapsto\frac{x(x^4-6x^2-4ax^3-3)^2}{(3x^4+4ax^3+6x^2-1)^2}
\] 通过令分母等于\(0\)我们可以得到四个根\(\beta,\delta,\zeta,\theta\),通过这四个根我们可以得到八个阶为\(3\)的点:\((\beta,\pm\gamma),(\delta,\pm\epsilon),(\zeta,\pm\eta),(\theta,\pm\iota)\),这八个点加上无穷远点可以构成子群\(\ker([3])\simeq\mathbb{Z}_3\times\mathbb{Z}_3\),也可以叫做\(3\)-torsion,\(3\)-torsion的结构如下图所示:
在这里每个“花瓣”对应一个二阶循环子群。相应的,还有三倍点映射\([3]\),对于蒙哥马利曲线\(E:y^2=x^3+ax^2+x\),其对应三倍点映射为: \[
[3]:E\mapsto E:x\mapsto\frac{x(x^4-6x^2-4ax^3-3)^2}{(3x^4+4ax^3+6x^2-1)^2}
\] 通过令分母等于\(0\)我们可以得到四个根\(\beta,\delta,\zeta,\theta\),通过这四个根我们可以得到八个阶为\(3\)的点:\((\beta,\pm\gamma),(\delta,\pm\epsilon),(\zeta,\pm\eta),(\theta,\pm\iota)\),这八个点加上无穷远点可以构成子群\(\ker([3])\simeq\mathbb{Z}_3\times\mathbb{Z}_3\),也可以叫做\(3\)-torsion,\(3\)-torsion的结构如下图所示: 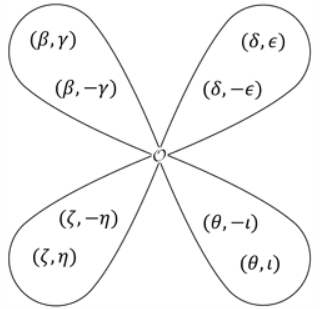
这里每个“花瓣”对应一个三阶循环子群。推广到一般情况,所有阶为\(l\)的点(\(p\nmid l\))与\(\mathcal{O}\)构成的子群就是\(\ker([l])\simeq \mathbb{Z}_l\times\mathbb{Z}_l\)(或者称为\(l\)-torsion),而若\(l\)为质数,则可以得到\(l+1\)个\(l\)阶循环子群
可分同源
可分同源的定义为对于一条曲线\(E\)上的椭圆曲线群以及它的一个子群\(G\),可以构造出唯一的同源\(\phi:E\mapsto E'\),使得\(\ker(\phi)=G\),这样得到的曲线\(E'\)称为该同源的陪域(codomain),可以表示为\(E/G\)。可分同源的另一种定义(Velu's formulas)是:输入一条椭圆曲线\(E\)以及其子群\(G\)的所有点,输出陪域\(E/G\)以及对应的映射\(\phi\)。
由于\(\ker(\phi)=G\),所以对于任意点\(P\in G\),都有\(\phi(P)=\mathcal{O}\)
以蒙哥马利曲线\(E:y^2=x^3+ax^2+x\)为例,设其上一个二阶子群为\(G=\{\mathcal{O},(\alpha,0)\}\),我们可以以\(G,E\)作为输入,得到映射\(\phi\): \[
\phi:x\mapsto\frac{x(\alpha x-1)}{x-\alpha}
\] 以及陪域\(E':y^2=x^3+2(1-2\alpha^2)x^2+x\),这个映射被用于计算蒙哥马利曲线的2-同源(2-isogeny),对\(GF(431^2)\)下的超奇异曲线\(E:y^2=x^3+(208i+161)x^2+x\),我们知道\(j(E)=364i+304\),则可以通过如下代码求得其一个\(2\)-同源并确保其输出的陪域为蒙哥马利曲线: p = 431
R.<i> = GF(p^2, modulus=[1, 0, 1])
E = EllipticCurve(R, [0, 208*i+161, 0, 1, 0])
ker2 = E(0).division_points(2)
# [(0 : 1 : 0), (0 : 0 : 1), (350*i + 68 : 0 : 1), (304*i + 202 : 0 : 1)]
alpha = ker2[2]
phi = E.isogeny(alpha, model = "montgomery")
print(phi.rational_maps())
print()
E_ = phi.codomain()
print(E_)
print(E_.j_invariant())
\(d\)-同源
对于同源\(\phi\),我们称\(|\ker(\phi)|\)为同源的度,度为\(d\)的同源称为\(d\)-同源,例如前面提到的\(2\)-同源.
sage上的同源
我们一般用sage的isogeny方法来计算同源,其函数原型如下: isogeny(_kernel_, _codomain=None_, _degree=None_, _model=None_, _check=True_, _algorithm=None_, _velu_sqrt_bound=None_)
_kernel_:就是前面提到输入的\(G\),可以是一个点,可以是点列,也可以是本原核多项式codomain:陪域,输入为一条椭圆曲线,这样生成的同源的陪域就是这条椭圆曲线model:输出的陪域的形式,有三种可选参数:
'minimal',输出全局最小的椭圆曲线'short_weierstrass',输出short Weierstrass曲线,即由\(y^2=x^3+ax+b\)形式的方程所定义的椭圆曲线'montgomery'输出蒙哥马利曲线
algorithm:算法,有三种可选参数(均为自己的理解,可能不准确):
'velusqrt',使用平方根Vélu算法'factored',将度分解到为质因子之后再求解'traditional',传统算法
同源图(Isogeny graph)
对于一个固定的\(p\),我们用\(GF(p^2)\)中所有的超奇异\(j\)-不变量各构造一条曲线,在每条曲线的\(\ker([l])\)中取除了无穷远点外的所有点分别进行同源,将原来曲线的\(j\)-不变量作为起点,同源得到的陪域的\(j\)-不变量作为终点,就可以得到一个无向图,称为同源图,例如在参考资料2中给出的\(GF(431^2)\)下的\(\ker([2])\)的同源图: 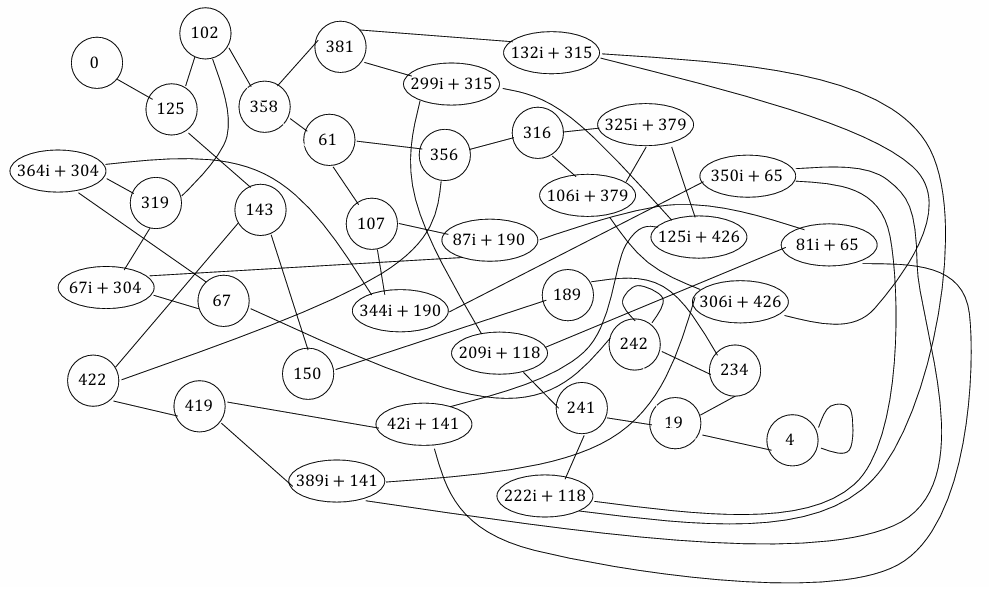 通过同源图,我们可以知道超奇异曲线的\(j\)-不变量在同源时的变化路线. 可以通过如下算法求\(GF(p^2)\)下的\(\ker([l])\)的同源图:
通过同源图,我们可以知道超奇异曲线的\(j\)-不变量在同源时的变化路线. 可以通过如下算法求\(GF(p^2)\)下的\(\ker([l])\)的同源图:
def IsogenyGraph(p, l=2, vertex_size=3750, size=[20, 20]): |
通过这个算法画出来的\(GF(431^2)\)下的\(\ker([2])\)的同源图长这样: 
超奇异同源Diffie-Hellman密钥交换体系(SIDH)
SIDH协议细节
首先密钥交换双方(以下称为Alice和Bob)协商选取模数\(p=2^a3^b-1\),其中\(2^a\approx 3^b\),然后选取一条\(GF(p^2)\)下的超奇异椭圆曲线\(E\),在此之后,Alice选取\(E\)上阶为\(2^a\)的两点\(P_A,Q_A\)并公开,Bob选取\(E\)上阶为\(3^b\)的两点\(P_B,Q_B\)并公开(在选取的时候,需要保证\(P_A,Q_A\)线性无关,\(P_B,Q_B\)线性无关)。 Alice随机选取秘密值\(k_A\in\{0,1,\cdots,2^a-1\}\),计算\(S_A=P_A+k_AQ_A\),并通过\(S_A\)计算同源\(\phi_A:E\mapsto E_A\),其中\(E_A=E/\langle S_A\rangle\),\(\phi_A\)由\(a\)个\(2\)-同源组合而成,最后使用\((E_A,\phi_A(P_B),\phi_A(Q_B))\)作为公钥,\((k_A,S_A)\)作为私钥; 同样的,Bob随机选取秘密值\(k_B\in\{0,1,\cdots,3^b-1\}\),计算\(S_B=P_B+k_BQ_B\),通过\(S_B\)计算同源\(\phi_B:E\mapsto E_B\),其中\(\phi_B\)由\(b\)个\(3\)-同源组合而成,使用\((E_B,\phi_B(P_A),\phi_B(Q_A))\)作为公钥,\((k_B,S_B)\)作为私钥。 通过上述计算得到的公钥,Alice可以计算出\(S_{A}'=\phi_B(P_A)+k_A\phi_B(Q_A)\),计算同源\(\phi_A':E_B\mapsto E_{AB}\),就可以计算出\(j_{AB}=j(E_{AB})\),同样的,Bob可以计算出\(S_{B}'=\phi_A(P_B)+k_B\phi_A(Q_B)\),然后计算同源\(\phi_B':E_A\mapsto E_{BA}\),从而可以计算出\(j_{BA}=j(E_{BA})\),有\(j_{AB}=j_{BA}\),所以共享密钥值为\(j=j_{AB}=j_{BA}\).
SIDH实例
本样例来源于参考资料2
Alice和Bob协商选取模数\(p=2^43^3-1=431\),并选取\(GF(p^2)\)上的一条超奇异椭圆曲线: \[
E:y^2=x^3+(329i+423)x^2+x
\] 有\(j(E)=87i+190\),Alice从中选取两个阶为\(2^4\)的点: \[
P_A=(100i+248,304i+199),Q_A=(426i+394,51i+79)
\] 同时Bob从中选取两个阶为\(3^3\)的点: \[
P_B = (358i+275, 410i+104),Q_B = (20i+185, 281i+239)
\] p = 2^4 * 3^3 - 1
R.<i> = GF(p^2, modulus=[1, 0, 1])
a = 329*i + 423
E = EllipticCurve(R, [0, a, 0, 1, 0])
PA = E(100*i+248, 304*i+199)
QA = E(426*i+394, 51*i+79)
assert PA.order() == QA.order() == 2^4
PB = E(358*i+275, 410*i+104)
QB = E(20*i+185, 281*i+239)
assert PB.order() == QB.order() == 3^3 其中\(e\)表示恒等映射,sage代码如下:
其中\(e\)表示恒等映射,sage代码如下:
phis = [] |
计算得到\(E_A:y^2 = x^3 + (128i+19)x^2 + x\),\(\phi_A(P_B)=(130i + 170,428i + 290)\),\(\phi_A(Q_B)=(235i+209,126i+15)\); 同理,Bob在\(\{0,1,\cdots,3^3-1\}\)中选择\(k_B=2\),计算\(S_B=P_B+k_BQ_B=(122i +309, 291i+374)\),那么我们可以通过如下算法计算出\(S_B\)对应的同源:  其中\(e\)表示恒等映射,sage代码如下:
其中\(e\)表示恒等映射,sage代码如下:
phis = [] |
计算得到\(E_B:y^2 = x^3 + (329i+8)x^2 + x\),\(\phi_B(P_A)=(160i + 421, 246i + 252)\),\(\phi_B(Q_A)=(119i+14, 246i + 138)\) 这样双方的公钥均已经计算出来,最后Alice就可以通过自己的私钥计算出: \[
S_{A}'=\phi_B(P_A)+k_A\phi{(Q_A)}
\] 再通过上述算法计算出Alice侧\(S_{A}'\)对应的同源的陪域\(E_A/\langle S_{A}'\rangle\),那么这个陪域的\(j\)-不变量就是共享密钥,同样的,Bob可以通过自己的私钥计算出: \[
S_{B}'=\phi_A(P_B)+k_B\phi{(Q_A)}
\] 再通过上述算法计算出Bob侧\(S_{B}'\)对应的同源的陪域\(E_B/\langle S_{B}'\rangle\),那么这个陪域的\(j\)-不变量就是共享密钥,可以通过下列代码计算出共享密钥: SAB = phiA(PB) + kB * phiA(QB)
EAB = EA_.isogeny(SAB, model="montgomery").codomain()
Bob_shared_secret = EAB.j_invariant()
print(Bob_shared_secret)
SBA = phiB(PA) + kA * phiB(QA)
EBA = EB_.isogeny(SBA, model="montgomery").codomain()
Alice_shared_secret = EBA.j_invariant()
print(Alice_shared_secret)a = 4
b = 3
p = 2^a * 3^b - 1
R.<i> = GF(p^2, modulus=[1, 0, 1])
A = 329*i + 423
E = EllipticCurve(R, [0, A, 0, 1, 0])
PA = E(100*i+248, 304*i+199)
QA = E(426*i+394, 51*i+79)
PB = E(358*i+275, 410*i+104)
QB = E(20*i+185, 281*i+239)
assert PA.order() == QA.order() == 2^4 and PB.order() == QB.order() == 3^3
kA = 11
SA = PA + kA * QA
phiA = E.isogeny(SA, model="montgomery", algorithm="factored")
EA = phiA.codomain()
PB_ = phiA(PB)
QB_ = phiA(QB)
kB = 2
SB = PB + kB * QB
phiB = E.isogeny(SB, model="montgomery", algorithm="factored")
EB = phiB.codomain()
PA_ = phiB(PA)
QA_ = phiB(QA)
SAB = phiA(PB) + kB * phiA(QB)
EAB = EA.isogeny(SAB, model="montgomery", algorithm="factored").codomain()
Bob_shared_secret = EAB.j_invariant()
SBA = phiB(PA) + kA * phiB(QA)
EBA = EB.isogeny(SBA, model="montgomery", algorithm="factored").codomain()
Alice_shared_secret = EBA.j_invariant()
assert Bob_shared_secret == Alice_shared_secret
print(Alice_shared_secret)def gen_public_key(E, P1, Q1, s, P2, Q2):
S = P1 + s*Q1
phi = E.isogeny(S, model='montgomery', algorithm="factored")
return phi, (phi.codomain(), phi(P2), phi(Q2))
def gen_shared_secret(E, P, Q, s):
S = P + s*Q
phi1 = E.isogeny(S, model='montgomery', algorithm="factored")
return phi1.codomain().j_invariant()
SIDH的安全性
理论上SIDH的安全性主要依赖于通过公钥中给出的曲线来求出它对应的同源。但是在2022年SIDH就被宣布完全破解,在Github上就有代码:GiacomoPope/Castryck-Decru-SageMath: A SageMath implementation of the Castryck-Decru Key Recovery attack on SIDH,要用的话拔出来用就行
