已知两质因数半数以上随机位的大整数分解

在解决RSA问题的过程中，我们往往会需要对一个大整数\(n\)进行质因数分解，在已知部分连续位的时候，我们经常会考虑使用Copper Smith方法来进行分解，但是若我们知道的是随机分散的位，Copper Smith方法将会失效，例如我们知道由两个质因数相乘得到的一个大整数\(n=pq\)如下：

104158954646372695568095796310479805403678314919693272509836778997179683485437763692891984254171869987446475357518587344178264028334102088429629785065036660148146855007349113784322098795994839040721664806905084554147298456659074384855277678993200563966327086005547016327991986225930798076081014377904788085807

又已知\(p\)的部分已知位（二进制表示，其中下划线为未知位，下同）：

1010101111000___11000___11100___11010___0___0___0___100110000___0___0___0___11000___0___0___110110010___11001100100111010___100011000___0___0___0___11111000111111100___1101110010000___0___0___0___10110___0___0___0___0___0___1100101111000___0___1001111011110___0___10000___0___0___11010___1010101110110___0___0___0___0___10010___1011101011100___110111010___0___0___0___101010110___0___10000___1000101011000___0___0___0___101010000___11010___111010000___0___11110___0___10010___111010010___0___0___10100___0___0___

与\(q\)的部分已知位：

110111010___111011110___0___1000100110001110100111100___0___10110___11000___0___10110___11100___10000___0___0___11111100110010100___10000___11100___0___110010110___101110010___10010___11110___11110___0___1101111011000___101010110___10100___0___10100___1010101011010___0___0___100110110___0___10000___0___0___1000101110010___1111110010110___0___0___0___101110100___0___1100101111000___10100___0___0___0___0___0___0___10010___0___0___10100___10010___0___0___0___101011110___0___111110000___0___11110___0___10100___

显然，我们不能使用Copper Smith方法进行分解。

为应对这种情况，大佬y011d4在Github上发布了一个项目：y011d4/factor-from-random-known-bits，我们可以使用这个项目对上述的情况进行分解。

下载方法（推荐Linux）：

首先确保系统中有Rust环境（因为这个项目主要是由Rust语言编写的）
使用git clone https://github.com/y011d4/factor-from-random-known-bits.git从Github上将该项目拉下来
cd factor-from-random-known-bits进入项目文件夹后依次运行pip install -r requirements.txt以及python setup.py install

在此之后就可以通过在Python中import factor后使用这个方法进行分解了。

假若安装时报错，则有可能是系统中缺少 m4 这个宏处理器，可以通过sudo apt-get install m4来安装这个宏处理器.

适用条件

已知\(p\)和\(q\)各50%以上的位

使用方法

这个库有两种使用方法：from_str以及from_vector

`from_str`

以前面的数据为例，则可以通过如下代码对\(n\)进行分解：

import factor

n = 104158954646372695568095796310479805403678314919693272509836778997179683485437763692891984254171869987446475357518587344178264028334102088429629785065036660148146855007349113784322098795994839040721664806905084554147298456659074384855277678993200563966327086005547016327991986225930798076081014377904788085807
p_known = "1010101111000___11000___11100___11010___0___0___0___100110000___0___0___0___11000___0___0___110110010___11001100100111010___100011000___0___0___0___11111000111111100___1101110010000___0___0___0___10110___0___0___0___0___0___1100101111000___0___1001111011110___0___10000___0___0___11010___1010101110110___0___0___0___0___10010___1011101011100___110111010___0___0___0___101010110___0___10000___1000101011000___0___0___0___101010000___11010___111010000___0___11110___0___10010___111010010___0___0___10100___0___0___"
q_known = "110111010___111011110___0___1000100110001110100111100___0___10110___11000___0___10110___11100___10000___0___0___11111100110010100___10000___11100___0___110010110___101110010___10010___11110___11110___0___1101111011000___101010110___10100___0___10100___1010101011010___0___0___100110110___0___10000___0___0___1000101110010___1111110010110___0___0___0___101110100___0___1100101111000___10100___0___0___0___0___0___0___10010___0___0___10100___10010___0___0___0___101011110___0___111110000___0___11110___0___10100___"

p, q = factor.from_str(n, p_known, q_known)

print(f"{p = }")
print(f"{q = }")

运行可以得到：

p = 8996460061304658501483536370547552107653796408964122401908135206811298639114618429412462572834106148254319079697639081615546751035691609086377055207530819
q = 11577771027337574615881755252249566401199602697310825312674761422549781992489861876313558348484109945826438743090783573542794191930931862927421766237119653

在这里，我们将未知的位置为下划线。

`from_vector`

以前面的数据为例，也可以通过如下代码对\(n\)进行分解：

import factor

n = 104158954646372695568095796310479805403678314919693272509836778997179683485437763692891984254171869987446475357518587344178264028334102088429629785065036660148146855007349113784322098795994839040721664806905084554147298456659074384855277678993200563966327086005547016327991986225930798076081014377904788085807
p_known = [1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, -1, -1, -1, 1, 1, 0, 0, 0, -1, -1, -1, 1, 1, 1, 0, 0, -1, -1, -1, 1, 1, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, -1, -1, -1, 1, 0, 0, 0, 1, 1, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, -1, -1, -1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 1, 0, -1, -1, -1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, -1, -1, -1, 1, 1, 0, 1, 1, 1, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 1, 0, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 0, 0, -1, -1, -1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 1, 0, 0, 0, 0, -1, -1, -1, 1, 1, 0, 1, 0, -1, -1, -1, 1, 1, 1, 0, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 1, 1, 0, 1, 0, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1]

q_known = [1, 1, 0, 1, 1, 1, 0, 1, 0, -1, -1, -1, 1, 1, 1, 0, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 1, 0, -1, -1, -1, 1, 1, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 1, 0, -1, -1, -1, 1, 1, 1, 0, 0, -1, -1, -1, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, -1, -1, -1, 1, 0, 0, 0, 0, -1, -1, -1, 1, 1, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 0, 1, 0, 1, 1, 0, -1, -1, -1, 1, 0, 1, 1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 1, 1, 1, 0, -1, -1, -1, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, -1, -1, -1, 1, 0, 1, 0, 1, 0, 1, 1, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 1, 0, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, -1, -1, -1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 1, 1, 0, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1, 1, 0, 0, 1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 1, 1, 1, 0, 0, 0, 0, -1, -1, -1, 0, -1, -1, -1, 1, 1, 1, 1, 0, -1, -1, -1, 0, -1, -1, -1, 1, 0, 1, 0, 0, -1, -1, -1]

p, q = factor.from_str(n, p_known, q_known)

print(f"{p = }")
print(f"{q = }")

运行可以得到相同的结果。

在这种用法中，我们将未知的位设置为-1

注意：虽然适用条件中说已知\(p\)和\(q\)各50%以上的位就能使用，但是在某次测试中发现\(p\)与\(q\)均已知50.05%的位的时候其实是用不了的，这种时候就要通过爆破来知道尽可能多的位。

使用例：[BCACTF 5.0 Superstitious 2]

加密代码如下：

from Crypto.Util.number import *
def myGetPrime():
    while True:
        x = getRandomNBitInteger(1024) & ((1 << 1024) - 1)//3
        if isPrime(x):
            return x
p = myGetPrime()
q = myGetPrime()
n = p * q
e = 65537
message = open('flag.txt', 'rb')
m = bytes_to_long(message.read())
c = pow(m, e, n)
open("superstitious-2.txt", "w").write(f"n = {n}\ne = {e}\nc = {c}")

可以知道((1 << 1024) - 1)//3如下：

101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101

所以我们可以知道\(p\)以及\(q\)约半数的位为0，以及最低位为1（因为\(p\),\(q\)必为奇数），所以我们将除了最低位的所有1都替换为下划线后通过Cyberchef统计之后可以看到：

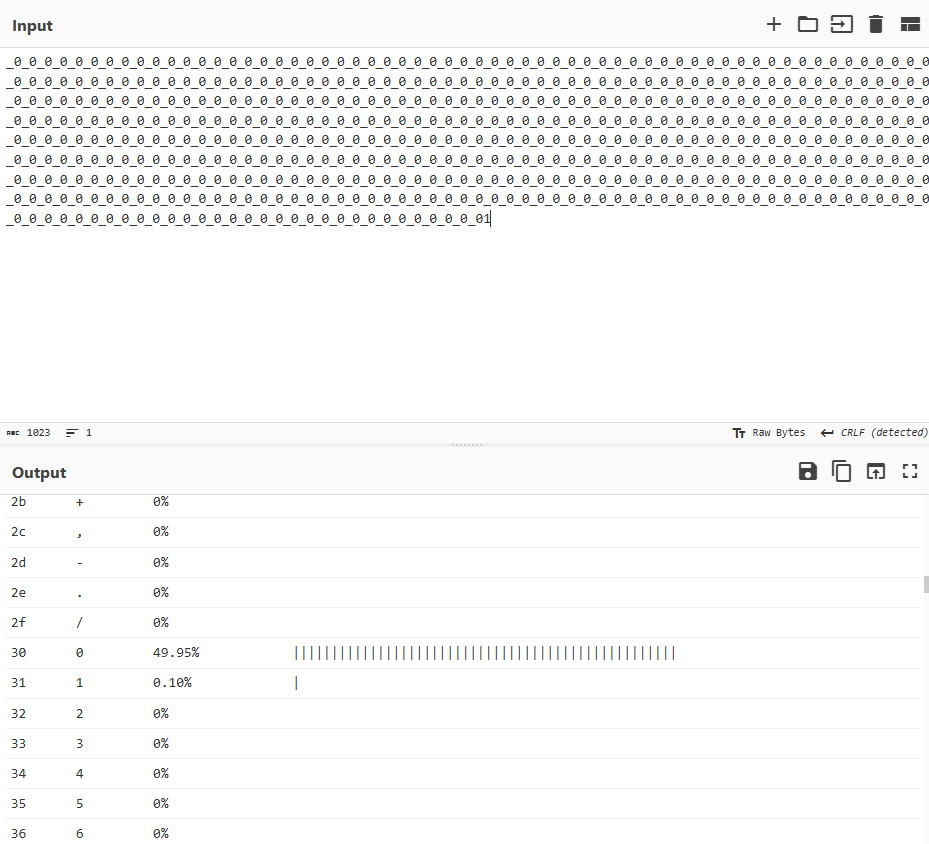
有50.05%的位已知，显然可以利用本文说的方法来进行分解，但是实际操作发现只知道这么多位并不能直接分解\(p\)和\(q\)，所以我们需要对\(p\)进行小范围爆破，所以我们可以通过如下脚本来进行求解：

from Crypto.Util.number import *
import tqdm
import factor

n = 550201148354755741271315125069984668413716061796183554308291706476140978529375848655819753667593579308959498512392008673328929157581219035186964125404507736120739215348759388064536447663960474781494820693212364523703341226714116205457869455356277737202439784607342540447463472816215050993875701429638490180199815506308698408730404219351173549572700738532419937183041379726568197333982735249868511771330859806268212026233242635600099895587053175025078998220267857284923478523586874031245098448804533507730432495577952519158565255345194711612376226297640371430160273971165373431548882970946865209008499974693758670929
e = 65537
c = 12785320910832143088122342957660384847883123024416376075086619647021969680401296902000223390419402987207599720081750892719692986089224687862496368722454869160470101334513312534671470957897816352186267364039566768347665078311312979099890672319750445450996125821736515659224070277556345919426352317110605563901547710417861311613471239486750428623317970117574821881877688142593093266784366282508041153548993479036139219677970329934829870592931817113498603787339747542136956697591131562660228145606363369396262955676629503331736406313979079546532031753085902491581634604928829965989997727970438591537519511620204387132

binlist = []
s = "_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_0_01"
for x in range(2**8):
    b = bin(x)[2:].rjust(8, '0')
    ns = list(s)
    for i in range(8):
        ns[2*i] = b[i]
    binlist.append("".join(ns))

for pknown in tqdm.tqdm(binlist):
    ps = factor.from_str(n, pknown, s)
    if ps != None:
        p, q = ps
        phi = (p - 1) * (q - 1)
        d = inverse(e, phi)
        m = pow(c, d, n)
        print(long_to_bytes(m))
        break

在这里，我们通过爆破\(p\)的高16位中的8个未知位将\(p\)的已知位提升了8位，将补充的位全部置0再进行统计可以看到：

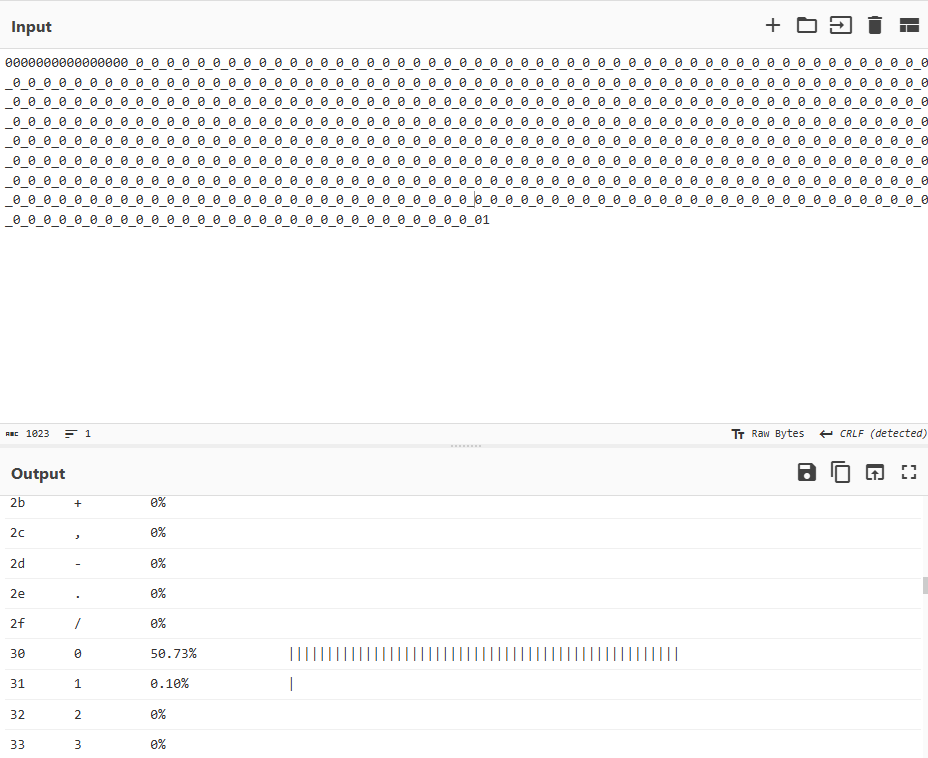
这时候\(p\)的已知部分变成了50.83%，应该可以进行有效分解了。运行脚本之后我们就可以得到flag：

bcactf{l4zy_cHall3nG3_WRITinG_f8b335319e464}